周邊昏暗

周邊昏暗是恆星因為密度由中心向邊緣逐漸降低而呈現出影像向邊緣的強度減少。周邊昏暗是兩種效應造成的結果：

恆星的密度由中心向外逐漸降低

恆星的溫度因為與中心距離的增加而逐漸降低。

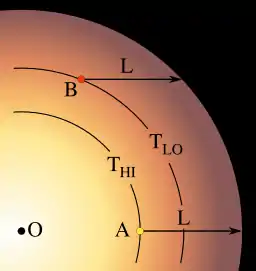
周邊昏暗的理想狀況。半徑的最外緣是來自恆星向外輻射的光子不再被吸收的區域，L 是光深度為1單位的距離。由A處輻射出的高溫光子和由B處輻射出的低溫光子都正好在可以逃脫的距離上。

周邊昏暗的太陽－以可見光觀察的太陽影像，因為密度向邊緣逐漸降低而在太陽盤面的外緣顯示出周邊昏暗的效應。

光深度的觀念是了解周邊昏暗的關鍵想法。光深度在光學上的1單位是由吸收氣體能逃逸出來的比率達到1/e光子數量的厚度。這是為何定義了恆星可見的邊緣之後，在光深度為1單位之處恆星就會變得不透明的原因。到達我們的輻射非常接近恆星釋放出的能量沿著視線方向朝向我們，直至光深度為1單位處點的總量。當我們觀察恆星的邊緣時，我們不能看見如同觀察中心一樣的光深度，因為當觀測邊緣時，視線是以傾斜的角度在恆星的氣體中行進。換言之，當我們觀察太陽時，1光深度單位對應的長度在移向邊緣時會逐漸增加。

第二個作用的事實是，恆星大氣的有效溫度（通常）是隨著相對於中心距離的增加而降低。來自氣體的輻射放射與溫度的增加又強列的關聯性，例如，對一個黑體而言，強度與溫度的四次方成正比（斯特凡-波茲曼定律）。因此當我們觀察一顆恆星時，輻射來自光深度最接近1單位的點。而相較於觀察恆星的邊緣，這一點在觀察恆星中心點時，越是深入溫度就越高，強度也就越大。

事實上，我們太陽內部的溫度並不是隨著距離的增加而均勻的衰減，來自譜線的證據顯示每個區域的光深度與溫度有關。在這種情況下我們能看見周邊昏暗的現象。

周邊昏暗的計算

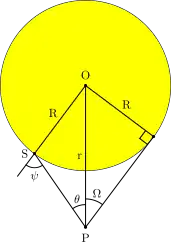
幾何學上的周邊昏暗。恆星的中心點在O ,半徑為R ，觀測者位於P 點，與中心的距離為r ；觀看表面的一個點S ，與中心連線的夾角為θ ，與恆星邊緣（或周邊）的夾角為Ω。

如右圖所示，沿著在大氣層之外的觀測者的點P，觀察方向為θ的強度只是角度ψ的函數，cos(ψ)的多項式是最接近與最方便的解。

{\frac {I(\psi )}{I(0)}}=\sum _{k=0}^{N}a_{k}\,{\textrm {cos}}^{k}(\psi )

此處， I_(ψ)是在P點看沿著視線與中心形成角度為ψ之處的強度，I₍₀₎是中心點的強度。可以看出，當ψ=0時，單位為1，因此我們必可得到：

\sum _{k=0}^{N}a_{k}=1

例如，從朗伯輻射體（沒有周邊昏暗），我們可以得到得到,除了a₀=1之外，所有的a_k=0。另一個例子，在550奈米的太陽，周邊昏暗可以用N=2來表示，並且

a_{0}=1-a_{1}-a_{2}\,

a_{1}=0.93\,

a_{2}=-0.23\,

（參考Cox, 2000）。註－周邊昏暗方程式有時也會寫成：

{\frac {I(\psi )}{I(0)}}=1+\sum _{k=1}^{N}A_{k}\,(1-\cos(\psi ))^{k}

在此處的N 相較於N+1 是獨立的函數，並且其總和為1單位。

我們能利用下面的關係式將ψ轉換為θ：

\cos(\psi )={\frac {\sqrt {\cos ^{2}(\theta )-\cos ^{2}(\Omega )}}{\sin(\Omega )}}

此處的Ω是觀測者至恆星邊緣的角度。

上面的近似可以用於獲得分析表示為中心強度的平均強度比率。平均強度I_m是在恆星盤面上包含立體角劃分的積分：

I_{m}={\frac {\int I(\psi )d\omega }{\int d\omega }}

此處，dω=sin(θ)dθdψ，是立體角的元素，在盤面上的積分為：0≤ψ≤2π和0≤θ≤Ω。雖然這個方程式可以分析來求解，但其仍是相當複雜的。當觀測者在很遙遠的距離上觀察天體時，上述的等式可以簡化為：

{\frac {I_{m}}{I(0)}}=2\sum _{k=0}^{N}{\frac {a_{k}}{k+2}}

參考資料

Billings, Donald E. . Academic Press, New York. 1966.
Cox, Arthur N. (ed). 14th ed. Springer-Verlag, NY. 2000. ISBN 0-387-98746-0.
Milne, E.A. MNRAS. 1921, 81: 361–375. 缺少或|title=为空 (帮助)
Minnaert, M. Z.f. Ap. 1930, 1: 209. 缺少或|title=为空 (帮助)
Neckel, H. and Labs, D. . Solar Physics. 1994, 153: 91–114.
van de Hulst, H. C. Bull. Astron. Inst. Netherlands. 1950, 11 (410): 135. 缺少或|title=为空 (帮助)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.