二极管模型

肖克利二极管方程建立了PN结二极管的电流${\displaystyle I}$和电压${\displaystyle V_{D}}$ 的关系。这个关系是在二极管的伏安特性：

${\displaystyle I=I_{S}\left(e^{V_{D}/(nV_{T})}-1\right)}$,

其中${\displaystyle I_{S}}$是二极管的饱和电流 或界电流 （其大小为电压${\displaystyle V_{D}}$在负方向超过${\displaystyle V_{T}}$的几倍时流过电流的大小，通常为10 ^-12 A）。反向饱和电流正比于二极管的横截面面积。其余符号的意思： ${\displaystyle V_{T}}$是热电压 （ ${\displaystyle kT/q}$ ，在常温下大约是26 mV），而${\displaystyle n}$被称为二极管理想因子（对于硅二极管${\displaystyle n}$约是1~2）。

当${\displaystyle V_{D}\gg nV_{T}}$时，该公式可以简化为：

${\displaystyle I\approx I_{S}\cdot e^{V_{D}/(nV_{T})}}$.

然而这个表达式只是更复杂的伏安特性的近似。在超浅结的情况下适用性特别受到限制，对于这种情况有更好的分析模型存在。[1]

为了说明在使用该法的复杂性，考虑求图1中二极管两端的电压这个问题。

图1：有阻性负载的二极管电路。

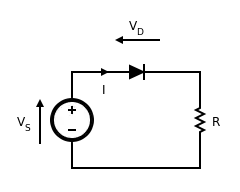
因为流过二极管的电流与流过整个电路的是相同的电流，我们可以列另一个方程。通过基尔霍夫定律知道，流过电路的电流

${\displaystyle I={\frac {V_{S}-V_{D}}{R}}}$.

这两个方程可以确定二极管的电流和二极管的电压。为了求解这两个方程，我们可以把第二个方程的${\displaystyle I}$代入第一个方程，然后尝试重新整理所得的方程来得到${\displaystyle V_{D}}$关于${\displaystyle V_{S}}$的函数。这种方法的一个困难是，在二极管定律是非线性的。然而，可以使用朗勃 ${\displaystyle W}$函数 得到一个不涉及${\displaystyle V_{D}}$的直接用${\displaystyle V_{S}}$表示${\displaystyle I}$的式子，这个式子是${\displaystyle f(w)=we^{w}}$的反函数，即, ${\displaystyle w=W(f)}$。接下来会讨论该解法。

图解分析法是一种简单的方法来得出一个数值解描述了二极管的超越方程。与大多数图解法一样，它具有简单、可视化的优点。通过绘制在伏安 曲线，因此能够得到的近似解的精度的任意程度。这个过程就是前面两种方法的图形等价，更适合于计算机实现。

这种方法在图上绘制两个电流 - 电压方程，两条曲线的交点同时满足这两个方程，从而得出流过电路的电流和二极管两端的电压的值。下图演示了这种方法。

通过二极管特性曲线与电阻性负载直线的交点确定静态工作点。

在实践中，图形方法对于复杂电路是复杂且不切实际的。二极管的另一种建模方法被称为分段线性 （PWL） 模型 。在数学上，这意味着把一个函数分解成若干直线段。这个方法用一系列线性段来近似二极管特性曲线。模型将真正的二极管表示为3部分串联：理想二极管、电压源和电阻器 。下图显示了一个真正的二极管的伏安曲线被近似为两段分段线性模型。通常会选择与二极管曲线相切于Q点（静态工作点）的倾斜线段。于是该线的斜率可以通过在Q点的二极管的小信号电阻的倒数给出。

二极管特性的分段线性逼近。

首先，让我们考虑一个数学理想化二极管。在这样一种理想的二极管中，如果二极管被反向偏置时，流过它的电流是零。这个理想二极管开始导通，在0 V和为任意的正电压无限流过电流，二极管的作用类似于短路。一个理想二极管的伏安特性如下所示：

理想二极管的伏安特性。

现在让我们考虑添加一个以如下方式与二极管串联的电压源的情况：

理想二极管串联一电压源。

理想的二极管正向偏置时是短路，而反向偏置时形成开路。 如果上述二极管的阳极连接到0V，阴极处的电压将为Vt ，那么阴极电位会高于阳极电位，二极管会被反向偏置。为了让该二极管导通，阳极上的电压应取Vt 。这个电路近似了存在于真实二极管的导通电压（也成开启电压）。该电路组合起来的伏安特性如下所示：

理想二极管和电压源串联的伏安特性。

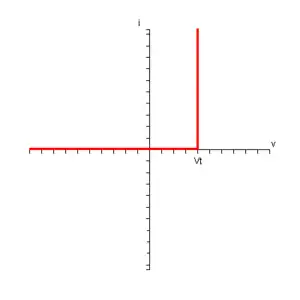
肖克莱二极管模型可以用于估算${\displaystyle V_{t}}$的近似值。

${\displaystyle I=I_{S}\left(e^{V_{D}/(n\cdot V_{T})}-1\right)\Leftrightarrow }$

${\displaystyle \ln \left(1+{\frac {I}{I_{S}}}\right)={\frac {V_{D}}{n\cdot V_{T}}}\Leftrightarrow }$

${\displaystyle V_{D}=n\cdot V_{T}\ln \left(1+{\frac {I}{I_{S}}}\right)\approx n\cdot V_{T}\ln \left({\frac {I}{I_{S}}}\right)\Leftrightarrow }$

${\displaystyle V_{D}\approx n\cdot V_{T}\cdot \ln {10}\cdot \log _{10}{\left({\frac {I}{I_{S}}}\right)}}$

使用${\displaystyle n=1}$和${\displaystyle T=25\,^{\circ }\!{\text{C}}}$ ：

${\displaystyle V_{D}\approx 0.05916\cdot \log _{10}{\left({\frac {I}{I_{S}}}\right)}}$

饱和电流在室温下的典型值是：

• ${\displaystyle I_{S}=10^{-12}}$硅二极管;
• ${\displaystyle I_{S}=10^{-6}}$锗二极管。

由于${\displaystyle V_{D}}$会随着${\displaystyle {\frac {I}{I_{S}}}}$的对数变化而变化，在这个比值变化比较大的时候${\displaystyle V_{D}}$的值变化非常小。利用10为底的对数可以更容易地 看出数量级的差异。

对于1.0 mA的电流：

• 硅二极管的${\displaystyle V_{D}\approx 0.53V}$（9个数量级）；
• 锗二极管的${\displaystyle V_{D}\approx 0.18V}$（3个数量级）。

对于100 mA的电流：

• 硅二极管的${\displaystyle V_{D}\approx 0.65V}$（11个数量级）;
• 锗二极管的${\displaystyle V_{D}\approx 0.30V}$（5个数量级）。

常用的硅二极管的值为0.6或0.7伏特[2]

需要做的最后一件事是用一个电阻来限制电流，如下图所示：

理想二极管串联电压源和电阻。

最终电路的伏安 特性如下：

理想二极管串联电压源和电阻的伏安特性。

真正的二极管，现在可以被替换的组合理想二极管、电压源和电阻器，然后就可以仅仅使用线性元素对电路建模。如果倾斜线段与真实二极管曲线相切于Q点，该近似电路具有与在Q点（静态工作点）的真实二极管相同的小信号电路。

运用肖克莱方程，可以导出二极管在某工作点（Q点）的小信号二极管电阻${\displaystyle r_{D}}$，其中的直流偏置电流为${\displaystyle I_{Q}}$和Q点施加的电压${\displaystyle V_{Q}}$ 。 [3] 首先，可以算出二极管的小信号电导 ${\displaystyle g_{D}}$，也就是二极管两端的电压的变化较小时引起的二极管电流的变化，除以电压的变化量为：

${\displaystyle g_{D}={\frac {\mathrm {d} I}{\mathrm {d} V}}{\Big |}_{Q}={\frac {I_{s}}{V_{T}}}e^{V_{Q}/V_{T}}\approx {\frac {I_{Q}}{V_{T}}}}$.

上式中最后的近似是由于假定偏置电流${\displaystyle I_{Q}}$足够大，可以使的肖克莱二极管方程的括号内的系数1忽略不计。这种逼近即使在相当低的电压时也是准确的，因为在300K的热电压 ${\displaystyle V_{T}\approx 25\,\mathrm {mV} }$，所以${\displaystyle V_{Q}/V_{T}}$就会比较大，这意味着该指数函数是非常大的。

注意到小信号电阻${\displaystyle r_{D}}$是刚才得到的小信号电导的倒数，二极管的电阻是独立于交流电流的，但却取决于直流电流，写作

${\displaystyle r_{D}={\frac {n\cdot V_{T}}{I_{Q}}}}$.