哈爾小波

${\displaystyle \psi (t)=\phi (2t)-\phi (2t-1)}$

${\displaystyle \psi (2t)}$

${\displaystyle \psi (2^{m}t-n)}$

由圖示可知：

(1):

${\displaystyle \Rightarrow \int \psi (t)\psi (2t)\,dt=0}$

${\displaystyle \int \psi (t)\psi (4t)\,dt=0}$

${\displaystyle \int \psi (2^{m}t)\psi (2^{m1}t)\,dt=0}$

(2):

${\displaystyle \Rightarrow \int \psi (t)\psi (t-1)\,dt=0}$

${\displaystyle \int \psi (t)\psi (2t-1)\,dt=0}$

${\displaystyle \int \psi (t)\psi (2^{m}-1)\,dt=0}$

scaling function

${\displaystyle \phi (t)}$

${\displaystyle \phi (2t),2\phi (2t)=\phi (t)+\psi (t)}$

${\displaystyle \psi (2^{m}t-n)}$

哈爾小波具有如下的特性：

(1)任何 function 都可以由 ${\displaystyle \phi (t),\phi (2t),\phi (4t),\dots ,\phi (2^{k}t)}$以及它們的位移所組成。

(2)任何平均為 0 的function 都可以由 ${\displaystyle \psi (t),\psi (2t),\psi (4t),\dots ,\psi (2^{k}t)}$所組成，也就是，任何 function 都可以由 常數, ${\displaystyle \psi (t),\psi (2t),\psi (4t),\dots ,\psi (2^{k}t)}$所組成。

(3)正交性(Orthogonal) ${\displaystyle \int _{-\infty }^{\infty }2^{m}\psi (2^{m_{1}}t-n_{1})\psi (2^{m}t-n)\,dt=\delta (m,m_{1})\delta (n,n_{1})}$

(4)不同寬度的(也就是不同 m) 的wavelet/scaling functions之間會有一個關係

 ${\displaystyle \phi (t)=\phi (2t)+\phi (2t-1)}$

${\displaystyle \phi (t-n)=\phi (2t-2n)+\phi (2t-2n-1)}$ ${\displaystyle \phi (2^{m}t-n)=\phi (2^{m+1}t-2n)+\phi (2^{m+1}t-2n-1)}$

 ${\displaystyle \psi (t)=\phi (2t)-\phi (2t-1)}$

${\displaystyle \psi (t-n)=\phi (2t-n)-\phi (2t-2n-1)}$ ${\displaystyle \psi (2^{m}t-n)=\phi (2^{m+1}t-n)-\phi (2^{m+1}t-2n-1)}$

(5)可以用 m+1的 係數来計算 m 的係數

若${\displaystyle \chi _{w}(n,m)=2^{m/2}\int _{-\infty }^{\infty }x(t)\phi (2^{m}t-n)\,dt}$

${\displaystyle {\begin{aligned}\chi _{w}(n,m)&=2^{m/2}\int _{-\infty }^{\infty }x(t)\phi (2^{m+1}t-2n)\,dt+\\&=2^{m/2}\int _{-\infty }^{\infty }x(t)\phi (2^{m+1}t-2n-1)\,dt\\&={\sqrt {\frac {1}{2}}}(\chi _{w}(2n,m+1)+\chi _{w}(2n+1,m+1))\\\end{aligned}}}$

若${\displaystyle \mathrm {X} _{w}(n,m)=2^{m/2}\int _{-\infty }^{\infty }x(t)\psi (2^{m}t-n)\,dt}$

${\displaystyle {\begin{aligned}\mathrm {X} _{w}(n,m)&=2^{m/2}\int _{-\infty }^{\infty }x(t)\phi (2^{m+1}t-2n)\,dt-\\&=2^{m/2}\int _{-\infty }^{\infty }x(t)\phi (2^{m+1}t-2n-1)\,dt\\&=\mathrm {X} _{w}(n,m)={\sqrt {\frac {1}{2}}}(\chi _{w}(2n,m+1)-\chi _{w}(2n+1,m+1))\\\end{aligned}}}$

圖示如下：

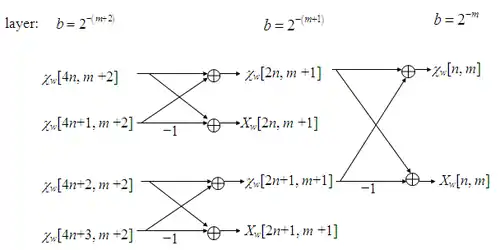
為多重解析結構(multiresolution analysis )

• Jian-Jiun Ding, Time frequency analysis and wavelet transform class note,the Department of Electrical Engineering, National Taiwan University (NTU), Taipei, Taiwan, 2013.
• Wavelets and subbands : fundamentals and applications/Agostino Abbate, Casimer M. DeCusatis, Pankaj K. Das.