幂集构造
在计算理论中,幂集构造是转换非确定有限状态自动机(NFA)到识别同样语言的确定有限状态自动机(DFA)的标准方法。它在理论上的重要性源于它确立了NFA尽管有额外的灵活性,它不能识别不能被任何DFA识别的任何语言。在实践中的重要性源于它把易于构造的NFA转换成了更有效执行的DFA。但是如果NFA有n个状态,结果的DFA可能有最多2n个状态,这种指数增长有时使这种构造对于大NFA而言是不实际的。
动机
回想一下,NFA除了特定节点可能有“分支”引出同时前进的多个路径之外,它和DFA是一样的。NFA将接受输入字符串,如果在计算完成的时候它的路径之一结束于一个接受状态。如果它的所有路径都失败,它就拒绝输入字符串。例如,在例子图中,如果我们在状态2而下一个输入符号是1,机器分支,行进到状态2和4二者。
注意不管NFA从一个状态中引出有多少不同的路径,它们每个在看到一个字符之后都必定到达n个状态中的一个。因此,给定以前的选择序列,我们可以简洁的总结NFA当前格局(configuration)为它在那个时刻可能处于的状态的集合。此外,我们如果我们知道NFA当前处在的状态的集合,我们可以指出基于下一个输入符号我们可以访问哪个状态集合。这就是算法的关键。
例子
考虑下列有字母表{0, 1}的NFA:
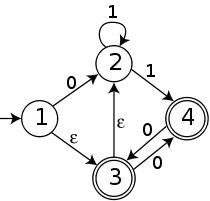
我们将构造一个等价的DFA;最终结果展示在后面。我们开始于开始状态。NFA开始于状态1,但是它可以不查看任何输入就沿着ε边前进到状态2和3。所以我们必须认为它最初同时处于这些状态。我们为DFA建立一个初始状态并标记上“{1,2,3}”。
接着,假设我们看到输入字符0。如果我们处在状态1,我们可以沿着标记0的边前进到状态2。如果我们处在状态3,我们可以前进到状态4。如果我们处在状态2,我们就被粘住了;没有0边出于状态2。这意味着NFA放弃从状态1沿着ε边到状态2的这条旧路径;它现在处在状态2和4之中。我们在DFA中增加从开始状态到标记着“{2,4}”的一个新状态的标记着“0”的一个新边。
假设我们最初看到的输入字符是1。则状态1的两个路径和状态3的路径不能前进,但状态2的路径可以并且它分支了:它同时保持在状态2和前进到状态4。因此,NFA现在在状态2和4中,就是说完全同于对0输入字符,但原因不同。我们在DFA中向从开始状态到现存的“{2,4}”状态的边增加标记“1”。
现在,假设我们在{2,4}状态并看见了字符1。在状态4中的路径不能前进,但是在状态2再次去到了2或4二者。我们仍在状态{2,4}中。如果我们看到了字符0,我们可以从从状态4前进到状态3,但不能从状态2前进到状态3。此外,在到达状态3之后,我们分支并也从ε-边到达状态2。结果是处在状态2和3。我们在DFA增加标记“{2,3}”的一个状态和从{2,4}到{2,3}的标记“0”的一个边。
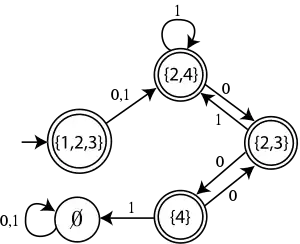
如果我们在状态{2,3}看到了字符1,状态3的路径不能前进,但是在状态2的路径前进到状态2和4,同前面一样这回到了节点{2,4}。如果我们看到字符0,状态2的路径不能继续,而在状态3的路径可以到达状态4。因此,我们只能到达状态4。我们在DFA中建立标记“{4}”的一个新状态和从{2,3}到{4}的标记“0”的一个边。
最后,如果我们在状态{4}并看到输入0,我们同前面一样前进到状态2和3,所以,在DFA中建立从{4}到{2,3}的一个标记“0”的边。如果我们看到了输入1,我们余下的所有路径都被粘住了而机器必须拒绝输入字符串。怎么办呢?我们在DFA中建立标记“”的新状态,从这里没有出路;所有它的外出边都指向自身,并且它不是接受状态。我们接着在DFA中增加从{4}到标记“1”的边。
现在我们已经考虑了所有可能情况。我们必须决定的是在这个DFA哪个状态应当接受。因为NFA接受输入字符串,如果任何它的路径结束于接受状态,我们可以通过设置所有包含接受NFA状态的DFA状态节点,为接受状态了模仿,也就是设置{1,2,3}, {2,3}, {2,4}和{4}为接受状态。结果的DFA完全接受同最初的NFA同样的字符串集合。注意这个DFA比最初的NFA更大。
定义DFA
我们来概括上述过程。定义一个DFA有四个重要问题必须回答:
- 什么是状态?
- 那些状态是接收状态?
- 什么状态是开始状态?
- 一个状态到下一个状态如何刻画?
我需要一个DFA的状态来描述NFA的每个可能格局。但是一般的说,NFA在任何给定点都可以处在它的状态的任何子集中。集合S的子集的集合叫做幂集,并写为P(S),我们定义在DFA中的状态集合是在NFA中状态集合的幂集。这回答了第一个问题。
我们已经提及了如果在NFA中任何并行路径在结束时处在接受状态,则NFA接受输入字符串。DFA可以通过在包含某NFA接受状态之一的任何状态中接受输入来模拟。这回答了第二个问题。
对于第三个问题。假设给NFA的输入字符串是空串。在它必须停止之前它可以访问什么状态?她不能沿着标记了输入符号的任何边前进,但它可以沿不消耗任何输入的ε边前进。因为它可以到达从开始状态之使用ε表到达的任何状态。这个状态集合形式上叫做开始状态的ε-闭包。因为我们的DFA在给予空输入串的时候时候除了立即停止不能做任何事情,我们必须保证DFA的开始状态包括所有可能的这些NFA状态。我们通过设置DFA的开始状态为NFA开始状态的ε-闭包来完成。
最后,我们使用类似的想法回答第四个问题。假设我们处在DFA的特定状态中(就是说,NFA状态的特定集合中)看到了特定输入符号,想知道下DFA的一个状态是什么。精确的回答是:从当前的NFA状态集合基于这个输入符号可以访问到NFA状态的集合。要得出这个集合,我们查看每一个NFA当前状态,并询问“给定这个输入符号,从这能到哪里呢?”。答案就是可沿着标记着这个输入符号的任何单一边,和任何数目的ε边前进。我们以这种方式查找并发现我们可以触及的所有节点,并把它们加入下一个状态的节点集合中。当我们对所有当前NFA状态完成了这个工作,我们就有了对应于特定DFA状态的NFA状态的集合,并增加从当前DFA状态到这个状态的标记着这个输入符号的一个边。
一旦我们已经对所有DFA状态和所有符号完成了这个过程,我们的DFA就完成了。结果的机器跟踪了NFA在输入字符串的每个时刻访问的状态的集合。但是,这个机器是非常大的:因为每个NFA的状态集合可能包含任何特定NFA状态,总共有2n这种集合,它们都是DFA可能有的节点。如果我们如例子中这样只建立必须的节点,我们经常会建立一个非常小的DFA的。不管如何,仍有必须所有2n个状态的情况,这是不可避免的。
形式定义
设M = (S, Σ, T, s, A)是非确定有限状态自动机。
定义5-元组Md = (Sd, Σd, Td, sd, Ad),这里的
- Sd = P(S)
- Σd = Σ
- sd = Cε(s)
- Td(q, a) = Cε(∪∀ r ∈ q T(r, a)) ∀q ∈ Sd, ∀ a ∈ Σ
- Ad = {q | q ∈ Sd ∧ q ∩ A ≠ ∅}
P(S)是S的幂集;
Cε(q)是 q的ε-闭包,就是说从q经过一次或多次ε-转移可到达的所有状态的集合。
可以数学上证明Md是接受同M一样语言的确定有限状态自动机。
引用
- Michael Sipser, Introduction to the Theory of Computation ISBN 0-534-94728-X. (See . Theorem 1.19, section 1.2, pg. 55.)
- John E. Hopcroft and Jeffrey D. Ullman, Introduction to Automata Theory, Languages and Computation, Addison-Wesley Publishing, Reading Massachusetts, 1979. ISBN 0-201-02988-X. (See chapter 2.)
