施瓦茨三角形

施瓦茨三角形所屬的空間取決於其p、q、r值：

${\displaystyle {\frac {1}{p}}+{\frac {1}{q}}+{\frac {1}{r}}>1{\text{$ : }}} 　球面

${\displaystyle {\frac {1}{p}}+{\frac {1}{q}}+{\frac {1}{r}}=1{\text{$ : }}} 　歐氏平面

${\displaystyle {\frac {1}{p}}+{\frac {1}{q}}+{\frac {1}{r}}<1{\text{$ : }}} 　羅氏平面（雙曲面）

施瓦茨三角形可以用三角圖來表示。每個節點表示施瓦茨三角形的邊（鏡射）。每條邊是由相應的反射階數合理的數值標示，即π/頂點角。

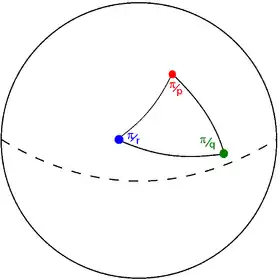Schwarz triangle (p q r) on sphere

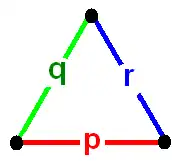Schwarz triangle graph

2階邊代表垂直於鏡射，可以在該圖中被忽略。在考克斯特 - 迪肯符號表示三角形圖中會隱藏2階邊。 考克斯特組可用於更簡單的符號，如(p q r)的循環圖，(p q 2) = [p,q](直角三角形)，和(p 2 2) = [p]×[].

• 埃里克·韦斯坦因. . MathWorld.
• Richard Klitzing, 3D, The general Schwarz triangle (p q r) and the generalized incidence matrices of the corresponding polyhedra