梯度下降法
梯度下降法(英語:)是一个一阶最优化算法,通常也称为最陡下降法,但是不該與近似積分的最陡下降法(英語:)混淆。 要使用梯度下降法找到一个函数的局部极小值,必须向函数上当前点对应梯度(或者是近似梯度)的反方向的规定步长距离点进行迭代搜索。如果相反地向梯度正方向迭代进行搜索,则会接近函数的局部极大值点;这个过程则被称为梯度上升法。
描述
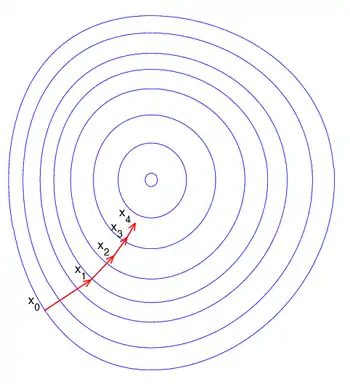
梯度下降法的描述。
梯度下降方法基于以下的观察:如果实值函数在点处可微且有定义,那么函数在点沿着梯度相反的方向 下降最多。
因而,如果
对于為一個够小数值時成立,那么。
考虑到这一点,我们可以从函数的局部极小值的初始估计出发,并考虑如下序列 使得
- 。
因此可得到
如果顺利的话序列收敛到期望的局部极小值。注意每次迭代步长可以改变。
右侧的图片示例了这一过程,这里假设定义在平面上,并且函数图像是一个碗形。蓝色的曲线是等高线(水平集),即函数为常数的集合构成的曲线。红色的箭头指向该点梯度的反方向。(一点处的梯度方向与通过该点的等高线垂直)。沿着梯度下降方向,将最终到达碗底,即函数局部極小值的点。
例子
梯度下降法处理一些复杂的非线性函数会出现问题,例如Rosenbrock函數
其最小值在处,数值为。但是此函数具有狭窄弯曲的山谷,最小值就在这些山谷之中,并且谷底很平。优化过程是之字形的向极小值点靠近,速度非常缓慢。
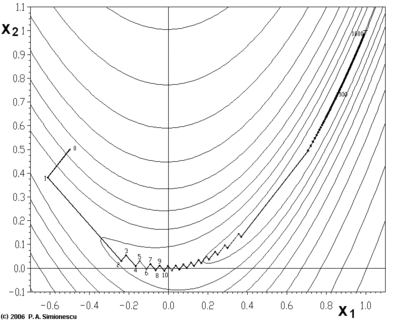
下面这个例子也鲜明的示例了"之字"的上升(非下降),这个例子用梯度上升(非梯度下降)法求的局部极大值(非局部极小值)。
.png.webp)
.png.webp)
参考文献
- David W. A. Bourne. . (原始内容存档于2009年2月10日) (英语).
- Mordecai Avriel (2003). Nonlinear Programming: Analysis and Methods. Dover Publishing. ISBN 0-486-43227-0.
- Jan A. Snyman (2005). Practical Mathematical Optimization: An Introduction to Basic Optimization Theory and Classical and New Gradient-Based Algorithms. Springer Publishing. ISBN 0-387-24348-8
外部链接
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
