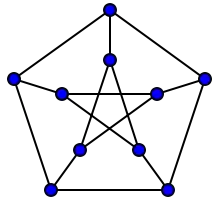
立方图
对称性
1932年,Ronald M. Foster首先寻找立方对称图的例子,并收集为Foster census。[1]许多著名的图都是立方对称图,如汤玛森图、彼得森图等。W. T. Tutte用满足下列性质的最大整数s来对立方对称图进行分类:图的自同构群在其所有长度为s的路径(其中不能有重复的边)组成的集合上作用是传递的。他证明了s最大只能取5,也即s的可能值是1到5。[2]
图着色与独立集
根据布鲁克定理,除了K4以外的任何连通立方图都可以用至多三种颜色染色。也即,这样的连通立方图至少存在一个包含n/3个顶点的独立集,其中n是该图的顶点数。
根据Vizing定理,任一立方图的边色数只能为三或四。3-边着色又称Tait-着色,Tait-着色方式将边集分割为三个完美匹配。根据Kőnig's_theorem每个二分立方图都有一个Tait-着色。
哈密顿回路
关于立方图是否具有哈密顿回路有许多研究。1880年,P.G. Tait猜想任一立方多面体图都有哈密顿回路。1946年,W. T. Tutte提出了Tait猜想的反例,有46个点的Tutte图。1971年,Tutte猜想所有的二分立方图都有哈密顿回路。然而Joseph Horton提出了Tutte猜想的反例,有96个点的Horton图。[3]在这之后,Mark Ellingham又提出了两个反例:Ellingham–Horton图。[4][5]Barnette猜想(目前仍是猜想)将Tait猜想与Tutte猜想结合起来,称任一二分立方多面体图都有哈密顿回路。当一个立方图有哈密顿回路时,可以使用LCF表示法简洁地表示。
如果从所有阶立方图中随机选取一个,那么它有相当大概率有哈密顿回路:当趋近于无穷时,这个概率趋近于1。[6]
David Eppstein猜想任一阶立方图最多有(约等于)条不同的哈密顿回路,且给出了极限情况下的例子。[7]目前为止,得到证明的最佳估计为。[8]
另见
- 一些简单的立方图
参考文献
- Foster, R. M., , Transactions of the American Institute of Electrical Engineers, 1932, 51 (2): 309–317, doi:10.1109/T-AIEE.1932.5056068.
- Tutte, W. T., , Can. J. Math., 1959, 11: 621–624, doi:10.4153/CJM-1959-057-2.
- Bondy, J. A. and Murty, U. S. R. Graph Theory with Applications. New York: North Holland, p. 240, 1976.
- Ellingham, M. N. "Non-Hamiltonian 3-Connected Cubic Partite Graphs."Research Report No. 28, Dept. of Math., Univ. Melbourne, Melbourne, 1981.
- Ellingham, M. N.; Horton, J. D., , Journal of Combinatorial Theory, Series B, 1983, 34 (3): 350–353, doi:10.1016/0095-8956(83)90046-1 已忽略未知参数
|doi-access=(帮助). - Robinson, R.W.; Wormald, N.C., , Random Structures and Algorithms, 1994, 5 (2): 363–374, doi:10.1002/rsa.3240050209.
- Eppstein, David, (PDF), Journal of Graph Algorithms and Applications, 2007, 11 (1): 61–81, arXiv:cs.DS/0302030, doi:10.7155/jgaa.00137.
- Gebauer, H., , , 2008.