補圖

在圖論裡面，一個圖G的補圖（complement）或者反面（inverse）是一個圖有著跟G相同的點，而且這些點之間有邊相連若且唯若在G裡面他們沒有邊相連。在製作圖的時候，你可以先建立一個有G所有點的完全圖，然後清除G裡面已經有的邊來得到補圖。這裡的補圖並不是圖本身的補集；因為只有邊的部份合乎補集的概念。

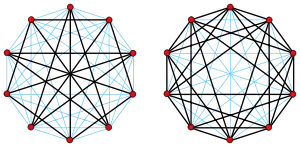
佩特森圖（左）以及其補圖（右）

正式建立法

令G = (V, E)是一個圖，K包含所有V的二元子集（2-element subset）。則圖H = (V, K \ E) 是G的補圖。

應用與範例

許多圖論的概念都互相以補圖的關係連接：

無邊圖的補圖是完全圖，反之亦然。
獨立集的補圖是团，反之亦然。
triangle-free graph的補圖是claw-free graph。
self-complementary graph是一個與自己的補圖同構的圖。
Cograph是由不交並（可參考集合論的的不交並）以及補集建立起來圖的集合。而且，這個集合是self-complementary；也就是說，任何cograph的補圖也必然是cograph（雖然可能不是同構的圖）。

參考資料

Bondy, John Adrian; Murty, U. S. R., , North-Holland, 1976, ISBN 0-444-19451-7, （原始内容存档于2010-04-13）, pages 6 and 29.

Diestel, Reinhard, 3rd, Springer, 2005, ISBN 3-540-26182-6. Electronic edition 页面存档备份，存于, page 4.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.