阻尼比
阻尼比(英語:)是工程上的無因次量,描述系統在受到擾動後振盪及衰減的情形。許多系統在受擾動,離開其靜平衡位置時都會振盪,例如吊在彈簧的重物,若用力往上拉再放開,就會上上下下的擺動。在擺動過程中,系統試圖回到平衡位置,不過會出現過沖。有時系統會有損耗(例如摩擦力)會形成系統的阻尼,會使系統的振盪漸漸變小,最後衰減。阻尼比是描述系統的振盪多快可以衰減。
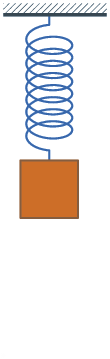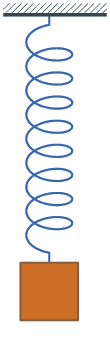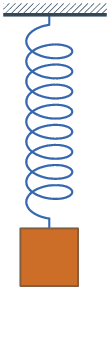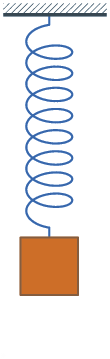
系統的振盪行為出現在許多不同的領域中,例如控制工程、機械工程、結構工程及電機工程等。振盪的物理量可能有很大的不同,振盪的可能是在大風中的建築物,也可能是馬達的速度,但利用正規化、無因次化的分析可以描述這些現象中共通的特性。
振盪情形
- 當彈簧質量系統完全沒有損耗,質量會一直擺動,不會結束,每一次的擺動振幅都和之前一樣,這種理想情形稱為無阻尼。
- 若系統的損耗很大,例如彈簧質量系統放置在黏滯的液體中,系統會慢慢的回到初始位置,甚至不會過沖,這稱為過阻尼。
- 一般而言,在擺動時會出現過沖,再往另一邊擺動,再回來,在擺動過程中,系統消耗了一些能量,而擺動振幅也會越來越小,最後回到初始位置,這稱為欠阻尼。
- 在過阻尼及欠阻尼二個條件之間,有一個特定的情形是系統不會過沖,會在最快時間回到初始位置,這稱為臨界阻尼。臨界阻尼和過阻尼都不會過沖,而臨界阻尼是最快回到初始位置的那一個阻尼條件。
定義

阻尼比常用ζ表示[1],是二階微分方程步階響應及頻率響應的參數之一。在控制理論及諧振子中相當重要。
阻尼比表示系統的阻尼相對於臨界阻尼的比值。若有阻尼的諧振子質量為m、阻尼係數為c、彈簧常數為k, 阻尼比可定義為系統的阻尼常數相對於臨界阻尼的比例:
若系統的運動方程為
其臨界阻尼係數為
或
阻尼比是二個相同單位係數的比值,因此為無因次量。
衍生
利用簡諧運動的自然頻率及以上的阻尼比定義,可以將二階微分方程式改寫如下:
上述方程式可以用以下的方式求解
其中C和s都是複數的常數。此解法假設解是振盪且/或指數遞減,將此放入微分方程中,可以得到振盪頻率的條件:
- 無阻尼:對應沒有阻尼的簡諧運動,其解為。
- 欠阻尼:若s為複數,解為指數遞減且振盪的函數,振盪部分可用表示。此時,稱為欠阻尼。
- 過阻尼:若s為實數,則解為沒有振盪的指數遞減,此時,稱為過阻尼。
- 臨界阻尼:當,介於過阻尼及欠阻尼之間,稱為臨界阻尼,這是許多工程應用想要的結果,也會希望阻尼振盪器可以設計在這一點。
品質因子及衰減速率
品質因子Q、阻尼比ζ及指數衰減率α有以下的關係[2]
若二階係系統的(欠阻尼系統),系統有二個共軛零點,其實部為,因此其指數衰減率參數表示振盪後指數衰減的速度。低阻尼比表示其衰減速度慢,因此許多欠阻尼的系統可以振盪較長的時間[3]。像高品質的音叉其阻尼比很小,因此敲擊後振盪可以持續很長的時間,衰減的速度很慢。
对数衰减
阻尼比也和欠阻尼系統中的对数衰减有關
上述關係只在欠阻尼的系統下有效,因為对数衰减定義為二個相鄰振幅比例的自然對數,而只有欠阻尼系統有振盪,才有對應的振幅。
相關條目
- 品質因子
- 衰減
