霍夫曼编码
霍夫曼編碼(英語:),又譯為哈夫曼编码、赫夫曼编码,是一種用於无损数据压缩的熵編碼(權編碼)演算法。由美國計算機科學家大衛·霍夫曼()在1952年發明。
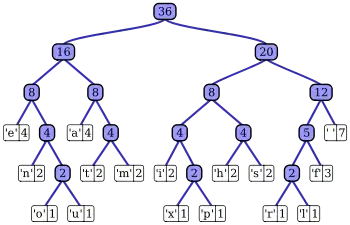
| 字母 | 頻率 | 編碼 |
|---|---|---|
| space | 7 | 111 |
| a | 4 | 010 |
| e | 4 | 000 |
| f | 3 | 1101 |
| h | 2 | 1010 |
| i | 2 | 1000 |
| m | 2 | 0111 |
| n | 2 | 0010 |
| s | 2 | 1011 |
| t | 2 | 0110 |
| l | 1 | 11001 |
| o | 1 | 00110 |
| p | 1 | 10011 |
| r | 1 | 11000 |
| u | 1 | 00111 |
| x | 1 | 10010 |
簡介
在计算机資料處理中,霍夫曼編碼使用變長編碼表對源符號(如文件中的一個字母)進行編碼,其中變長編碼表是通過一種評估來源符號出現機率的方法得到的,出現機率高的字母使用較短的編碼,反之出現機率低的則使用較長的編碼,這便使編碼之後的字符串的平均長度、期望值降低,從而達到無損壓縮數據的目的。
例如,在英文中,e的出現機率最高,而z的出現概率則最低。當利用霍夫曼編碼對一篇英文進行壓縮時,e極有可能用一個位元來表示,而z則可能花去25個位元(不是26)。用普通的表示方法時,每個英文字母均占用一個字節,即8個位元。二者相比,e使用了一般編碼的1/8的長度,z則使用了3倍多。倘若我們能實現對於英文中各個字母出現概率的較準確的估算,就可以大幅度提高無損壓縮的比例。
霍夫曼樹又稱最優二叉樹,是一種帶權路徑長度最短的二叉樹。所謂樹的帶權路徑長度,就是樹中所有的葉結點的權值乘上其到根結點的路徑長度(若根結點爲0層,葉結點到根結點的路徑長度爲葉結點的層數)。樹的路徑長度是從樹根到每一結點的路徑長度之和,記爲WPL=(W1*L1+W2*L2+W3*L3+...+Wn*Ln),N個權值Wi(i=1,2,...n)構成一棵有N個葉結點的二叉樹,相應的葉結點的路徑長度爲Li(i=1,2,...n)。可以證明霍夫曼樹的WPL是最小的。
歷史
1951年,霍夫曼在麻省理工學院(MIT)攻讀博士學位,他和修讀信息論課程的同學得選擇是完成學期報告還是期末考試。導師羅伯特·法諾(Robert Fano)出的學期報告題目是:尋找最有效的二進制編碼。由於無法證明哪個已有編碼是最有效的,霍夫曼放棄對已有編碼的研究,轉向新的探索,最終發現了基於有序頻率二叉樹編碼的想法,並很快證明了這個方法是最有效的。霍夫曼使用自底向上的方法構建二叉樹,避免了次優算法香農-范諾編碼(Shannon–Fano coding)的最大弊端──自頂向下構建樹。
1952年,於論文《一種構建極小多餘編碼的方法》()中發表了這個編碼方法。
問題定義與解法

廣義
- 給定
- 一組符號(Symbol)和其對應的權重值(weight),其權重通常表示成(%)。
- 欲知
- 一組二元的前置碼,其二元碼的長度為最短。
狹義
- 輸入
- 符號集合,其S集合的大小為。
- 權重集合,其W集合不為負數且。
- 輸出
- 一組編碼,其C集合是一組二進制編碼且為相對應的編碼,。
- 目標
- 設為的加權的路徑長,對所有編碼,則
範例
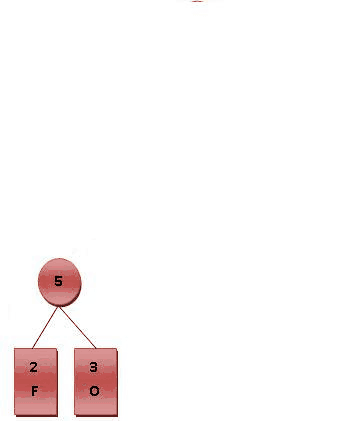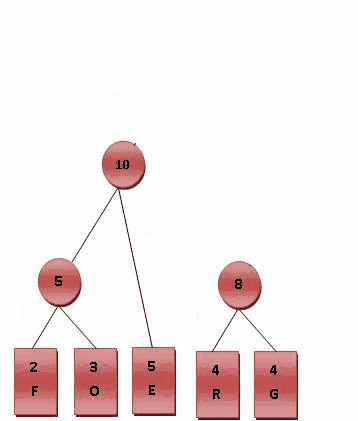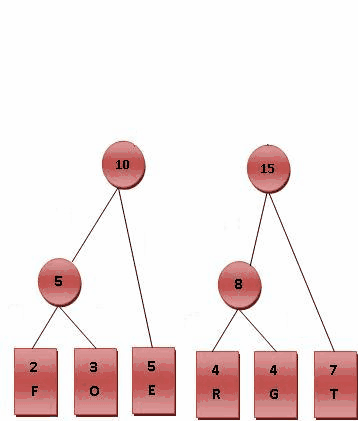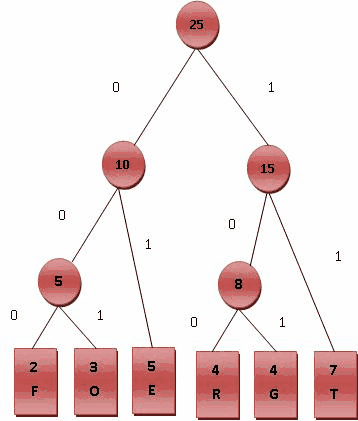
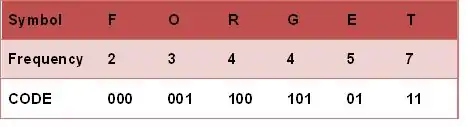
霍夫曼樹常處理符號編寫工作。根據整組資料中符號出現的頻率高低,決定如何給符號編碼。如果符號出現的頻率越高,則給符號的碼越短,相反符號的號碼越長。假設我們要給一個英文單字"F O R G E T"進行霍夫曼編碼,而每個英文字母出現的頻率分別列在Fig.1。
演算過程
(一)進行霍夫曼編碼前,我們先建立一個霍夫曼樹。
- ⒈將每個英文字母依照出現頻率由小排到大,最小在左,如Fig.1。
- ⒉每個字母都代表一個終端節點(葉節點),比較F.O.R.G.E.T六個字母中每個字母的出現頻率,將最小的兩個字母頻率相加合成一個新的節點。如Fig.2所示,發現F與O的頻率最小,故相加2+3=5。
- ⒊比較5.R.G.E.T,發現R與G的頻率最小,故相加4+4=8。
- ⒋比較5.8.E.T,發現5與E的頻率最小,故相加5+5=10。
- ⒌比較8.10.T,發現8與T的頻率最小,故相加8+7=15。
- ⒍最後剩10.15,沒有可以比較的對象,相加10+15=25。
最後產生的樹狀圖就是霍夫曼樹,參考Fig.2。
(二)進行編碼
- 1.給霍夫曼樹的所有左鏈結'0'與右鏈結'1'。
- 2.從樹根至樹葉依序記錄所有字母的編碼,如Fig.3。
實現方法
資料壓縮
實現霍夫曼編碼的方式主要是創建一個二元樹和其節點。這些樹的節點可以儲存在陣列裡,陣列的大小為符號(symbols)數的大小n,而節點分别是終端節點(葉節點)與非終端節點(內部節點)。
一開始,所有的節點都是終端節點,節點內有三個欄位:
1.符號(Symbol)
2.權重(Weight、Probabilities、Frequency)
3.指向父節點的鏈結(Link to its parent node)
而非終端節點內有四個欄位:
1.權重(Weight、Probabilities、Frequency)
2.指向兩個子節點的 鏈結(Links to two child node)
3.指向父節點的鏈結(Link to its parent node)
基本上,我們用'0'與'1'分別代表指向左子節點與右子節點,最後為完成的二元樹共有n個終端節點與n-1個非終端節點,去除了不必要的符號並產生最佳的編碼長度。
過程中,每個終端節點都包含著一個權重(Weight、Probabilities、Frequency),兩兩終端節點結合會產生一個新節點,新節點的權重是由兩個權重最小的終端節點權重之總和,並持續進行此過程直到只剩下一個節點為止。
實現霍夫曼樹的方式有很多種,可以使用優先佇列(Priority Queue)簡單達成這個過程,給與權重較低的符號較高的優先順序(Priority),演算法如下:
⒈把n個終端節點加入優先佇列,則n個節點都有一個優先權Pi,1 ≤ i ≤ n
⒉如果佇列內的節點數>1,則:
- ⑴從佇列中移除兩個最小的Pi節點,即連續做兩次remove(min(Pi), Priority_Queue)
- ⑵產生一個新節點,此節點為(1)之移除節點之父節點,而此節點的權重值為(1)兩節點之權重和
- ⑶把(2)產生之節點加入優先佇列中
⒊最後在優先佇列裡的點為樹的根節點(root)
而此演算法的時間複雜度( Time Complexity)為O(n log n);因為有n個終端節點,所以樹總共有2n-1個節點,使用優先佇列每個迴圈須O(log n)。
此外,有一個更快的方式使時間複雜度降至線性時間(Linear Time)O(n),就是使用兩個佇列(Queue)創件霍夫曼樹。第一個佇列用來儲存n個符號(即n個終端節點)的權重,第二個佇列用來儲存兩兩權重的合(即非終端節點)。此法可保證第二個佇列的前端(Front)權重永遠都是最小值,且方法如下:
⒈把n個終端節點加入第一個佇列(依照權重大小排列,最小在前端)
⒉如果佇列內的節點數>1,則:
- ⑴從佇列前端移除兩個最低權重的節點
- ⑵將(1)中移除的兩個節點權重相加合成一個新節點
- ⑶加入第二個佇列
⒊最後在第一個佇列的節點為根節點
雖然使用此方法比使用優先佇列的時間複雜度還低,但是注意此法的第1項,節點必須依照權重大小加入佇列中,如果節點加入順序不按大小,則需要經過排序,則至少花了O(n log n)的時間複雜度計算。
但是在不同的狀況考量下,時間複雜度並非是最重要的,如果我們今天考慮英文字母的出現頻率,變數n就是英文字母的26個字母,則使用哪一種演算法時間複雜度都不會影響很大,因為n不是一筆龐大的數字。
資料解壓縮
簡單來說,霍夫曼碼樹的解壓縮就是將得到的前置碼(Prefix Huffman code)轉換回符號,通常藉由樹的追蹤(Traversal),將接收到的位元串(Bits stream)一步一步還原。但是要追蹤樹之前,必須要先重建霍夫曼樹;某些情況下,如果每個符號的權重可以被事先預測,那麼霍夫曼樹就可以預先重建,並且儲存並重複使用,否則,傳送端必須預先傳送霍夫曼樹的相關資訊給接收端。
最簡單的方式,就是預先統計各符號的權重並加入至壓縮之位元串,但是此法的運算量花費相當大,並不適合實際的應用。若是使用Canonical encoding,則可精準得知樹重建的資料量只占B2^B位元(其中B為每個符號的位元數(bits))。如果簡單將接收到的位元串一個位元一個位元的重建,例如:'0'表示父節點,'1'表示終端節點,若每次讀取到1時,下8個位元則會被解讀是終端節點(假設資料為8-bit字母),則霍夫曼樹則可被重建,以此方法,資料量的大小可能為2~320位元組不等。雖然還有很多方法可以重建霍夫曼樹,但因為壓縮的資料串包含"trailing bits",所以還原時一定要考慮何時停止,不要還原到錯誤的值,如在資料壓縮時時加上每筆資料的長度等。
基本性質
考量到不同的應用領域以及該領域的平均性質,將會使用不同的通用機率,又或者,這個機率是可以從被壓縮文本中的實際頻率所取得。
最佳化
原始的霍夫曼演算法是一個符號與符號間已知輸入機率分佈的最佳編碼方式,也就是說將不相關的符號個別編碼為如此的資料串流。然而,當符號間的限制被捨棄或是質量機率函數是未知的時候,如此方式則並非最佳化。此外,當這些符號之間不是互相獨立,且分佈不相同的時候,單一一個符號可能不足以實現最佳化。在這種情況之下,算術編碼可能比起霍夫曼編碼會有更佳的壓縮能力。
雖然上述兩種方法都可以組合任意數量的符號以實現更高效的編碼效果,並且通常適應於實際的輸入統計層面,但儘管最簡單的版本比霍夫曼編碼更慢且更複雜,算術編碼不會顯著增加其計算或算法複雜度。當輸入概率不是精確已知或在流內顯著變化時,這種靈活性特別有用。然而,霍夫曼編碼通常更快,並且算術編碼在歷史上是專利問題的一些主題。因此,許多技術歷來避免使用有利於霍夫曼和其他前綴編碼技術的算術編碼。截至2010年中期,隨著早期專利的到期,這種替代霍夫曼編碼的最常用技術已經進入公有領域。
對於具有均勻概率分佈的一組符號,以及作為2的冪之成員,霍夫曼編碼等同於簡單的二進位制編碼,例如 ASCII 編碼。這反映了如此的事實:無論壓縮方法是什麼,這種輸入都不可能進行壓縮,或只是說對數據無所作為,比起壓縮才是才是最佳選擇。
在任何情況下,霍夫曼編碼在所有方法中是最佳的方式,其中每個輸入符號是具有二元機率的已知獨立且相同分佈的隨機變量。前綴碼,特別是霍夫曼編碼,往往在小字母表上產生較差的效率,其中概率通常落在這些最佳(二元)點之間。當最可能符號的概率遠超過0.5時,可能發生霍夫曼編碼的最壞情況,使低效率的上限無限制。
在使用霍夫曼編碼的同時,有兩種相關的方法可以解決這種特定的低效問題。將固定數量的符號組合在一起(阻塞)通常會增加(並且永不減少)壓縮。隨著塊的大小接近無窮大,霍夫曼編碼理論上接近熵限制,即最佳壓縮。然而,阻塞任意大的符號組是不切實際的,因為霍夫曼代碼的複雜性在要編碼的可能性的數量上是線性的,這是在塊的大小中呈指數的數字。這限制了在實踐中完成的阻塞量。
廣泛使用的實際替代方案是行程編碼。該技術在熵編碼之前增加一步,特別是對重複符號進行執行次數的計數,然後對其進行編碼。對於伯努力(Bernoulli)過程的簡單情況,哥倫(Golomb)編碼在編碼遊程長度的前綴碼中是最佳的,這是通過霍夫曼編碼技術證明的事實。使用改進的霍夫曼編碼的傳真機採用類似的方法。但是,遊程編碼並不像其他壓縮技術那樣適應許多輸入類型。
變化
霍夫曼編碼有衍生出許多的許多變化,其中一些使用類似霍夫曼的算法,而其他一些算法找到最佳前綴碼(例如,對輸出施加不同的限制)。注意,在後一種情況下,該方法不需要像霍夫曼那樣,實際上甚至不需要到多項式複雜度。
多元樹霍夫曼編碼
多元樹霍夫曼編碼演算法使用字母集 {0, 1, ... , n − 1} ,來構建一棵 n 元樹。霍夫曼在他的原始論文中考慮了這種方法。這與二進制(n=2)算法僅有的差別,就是它每次把 n 個最低權的符號合併,而不僅是兩個最低權的符號。倘若 n ≥ 2, 則並非所有源字集都可以正確地形成用於霍夫曼編碼的多元樹。在這些情況下,必須添加額外的零概率佔位符。這是因為該樹必須為滿的 n 叉樹,所以每次合併會令符號數恰好減少 (n -1), 故這樣的 n 叉樹存在當且僅當源字的數量模 (n -1) 餘 1. 對於二進制編碼,任何大小的集合都可以形成這樣的二叉樹,因為 n -1 = 1.
自適應霍夫曼編碼
自適應霍夫曼編碼的變化,涉及基於源符號序列中的最近實際頻率動態地計算概率,以及改變編碼樹結構以匹配更新的概率估計。它在實踐中很少使用,因為更新樹的成本使其比優化的自適應算術編碼慢,後者更靈活並且具有更好的壓縮。
霍夫曼模板演算法
在霍夫曼編碼的實現中,通常會使用權重表示數值概率,但是上面給出的算法不需要這樣;它只需要權重形成一個完全有序的可交換么半群,這意味著一種訂購權重和添加權重的方法。霍夫曼模板算法使人們能夠使用任何類型的權重(成本,頻率,權重對,非數字權重)和許多組合方法之一(不僅僅是加法),這個問題首先應用於電路設計。
長度限制霍夫曼編碼
長度受限的霍夫曼編碼是一種變體,其目標仍然是實現最小加權路徑長度,但是存在另外的限制,即每個碼字的長度必須小於給定常數。包合併算法通過一種與霍夫曼演算法非常相似的簡單貪婪方法解決了這個問題。
不相等成本霍夫曼編碼
在標準的霍夫曼編碼問題中,假設集合中構成碼字的每個符號具有相同的傳輸成本:長度為N位的碼字總是具有N的成本,無論多少這些數字是0,有多少是1,等等。在這個假設下工作時,最小化消息的總成本和最小化數字總數是相同的。
具有不等字母成本的霍夫曼編碼是沒有這種假設的概括:由於傳輸介質的特性,編碼字母表的字母可能具有不均勻的長度。一個例子是摩爾斯電碼的編碼字母表,其中'破折號'比'點'需要更長的發送時間,因此傳輸時間中破折號的成本更高。目標仍然是最小化加權平均碼字長度,但僅僅最小化消息使用的符號數量已經不夠了。沒有算法以與傳統霍夫曼編碼相同的方式或相同的效率來解決這個問題,儘管它已經由卡普(Karp)解決,其解決方案已經針對哥林(Golin)的整數成本的情況進行了改進。
最佳字母二元樹
在標準霍夫曼編碼問題中,假設任何碼字可以對應於任何輸入符號。在字母表中,輸入和輸出的字母順序必須相同。
規範霍夫曼編碼
如果對應於按字母順序排列的輸入的權重是按數字順序排列的,則霍夫曼代碼具有與最佳字母代碼相同的長度,這可以從計算這些長度中找到,從而不需要使用胡 - 塔克(Hu-Tucker)編碼。由數字(重新)有序輸入產生的代碼有時被稱為規範霍夫曼代碼,並且由於易於編碼/解碼,通常是實踐中使用的代碼。用於找到該代碼的技術有時被稱為霍夫曼 - 香農 - 法諾編碼,因為它像霍夫曼編碼一樣是最優的,但是在重量概率上是字母的,例如香農 - 法諾編碼。
資料長度
設符號集合,为發生的機率 ,为編碼的長度
- 熵(Entropy):亂度
ex:
第三與第四個範例,同樣是五種組合,機率分布越集中,則亂度越少
- 霍夫曼碼平均長度
- 霍夫曼碼的長度
- Shannon編碼定理: ≤ ≤ ,若使用進位的編碼
霍夫曼碼的平均編碼長度:設,為資料長度
- ≤ ≤
範例
- 當有100個位子,有白色佔60%、咖啡色佔20%,藍色和紅色各佔10%,則該如何分配才能最優化此座位?
(a)direct:
假設結果為:白色為00、咖啡色01,藍色10和紅色11個bits
則結果為:100*2 = 200bits
(b)huffman code: (must be satisfy the following conditions,if not change the node)
(1) 所有碼皆在Coding Tree的端點,再下去沒有分枝(滿足一致解碼跟瞬間解碼)
(2) 機率越大,code length越短;機率越小,code length越長
(3) 假設是第L層的node,是第L+1層的node
則必須滿足
假設結果為:白色佔0、咖啡色10,藍色110和紅色111個bits
則結果為:60*1+20*2+20*3=160bits
相互比較兩個結果huffman code 整整少了40bits的儲存空間。
示範程式
哈夫曼编码c代码
huffman.h文件
huffman.c文件:
程序演示主文件:
參考文獻
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Section 16.3, pp. 385–392.
外部連結
- 有關霍夫曼壓縮技術的原文:D.A. Huffman, "A method for the construction of minimum-redundancy codes", Proceedings of the I.R.E., sept 1952, pp 1098-1102
- 霍夫曼树图形演示
- Animation of the Huffman Algorithm: Algorithm Simulation by Simon Mescal
- Background story: Profile: David A. Huffman, Scientific American, Sept. 1991, pp. 54-58
- n-ary Huffman Template Algorithm
- Huffman codes' connection with Fibonacci and Lucas numbers
- Fibonacci connection between Huffman codes and Wythoff array
- Sloane A098950 Minimizing k-ordered sequences of maximum height Huffman tree
- Computing Huffman codes on a Turing Machine
- Mordecai J. Golin, Claire Kenyon, Neal E. Young "Huffman coding with unequal letter costs", STOC 2002: 785-791
- Huffman Coding, implemented in python