Trie
在计算机科学中,trie,又称前缀树或字典樹,是一种有序树,用于保存关联数组,其中的键通常是字符串。与二叉查找树不同,键不是直接保存在节点中,而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀,也就是这个节点对应的字符串,而根节点对应空字符串。一般情况下,不是所有的节点都有对应的值,只有叶子节点和部分内部节点所对应的键才有相关的值。
Trie这个术语来自于retrieval。根据词源学,trie的发明者Edward Fredkin把它读作/ˈtriː/ "tree"。[1][2]但是,其他作者把它读作/ˈtraɪ/ "try"。[1][2][3]
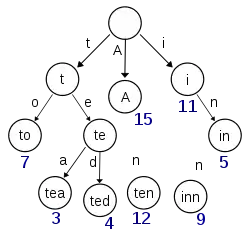
在图示中,键标注在节点中,值标注在节点之下。每一个完整的英文单词对应一个特定的整数。Trie可以看作是一个确定有限状态自动机,尽管边上的符号一般是隐含在分支的顺序中的。
键不需要被显式地保存在节点中。图示中标注出完整的单词,只是为了演示trie的原理。
trie中的键通常是字符串,但也可以是其它的结构。trie的算法可以很容易地修改为处理其它结构的有序序列,比如一串数字或者形状的排列。比如,bitwise trie中的键是一串位元,可以用于表示整数或者内存地址。
应用
trie树常用于搜索提示。如当输入一个网址,可以自动搜索出可能的选择。当没有完全匹配的搜索结果,可以返回前缀最相似的可能。[4]
实现方式
trie树实际上是一个确定有限状态自动机(DFA),通常用转移矩阵表示。行表示状态,列表示输入字符,(行,列)位置表示转移状态。这种方式的查询效率很高,但由于稀疏的现象严重,空间利用效率很低。也可以采用压缩的存储方式即链表来表示状态转移,但由于要线性查询,会造成效率低下。
于是人们提出了下面两种结构。[5]
三数组Trie
三数组Trie(Triple-Array Trie)结构包括三个数组:base,next和check.
二数组Trie
二数组Trie(Double-Array Trie)包含base和check两个数组。base数组的每个元素表示一个Trie节点,即一个状态;check数组表示某个状态的前驱状态。
实例
这是一个用于词频统计的程序范例,因使用了getline(3),所以需要glibc才能链接成功,没有glibc的话可以自行改写。
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define TREE_WIDTH 256
#define WORDLENMAX 128
struct trie_node_st {
int count;
int pass; //add a count for the part-include for example 'this is' then the 'is' is hited two times
struct trie_node_st *next[TREE_WIDTH];
};
static struct trie_node_st root={0, 0, {NULL}};
static const char *spaces=" \t\n/.\"\'()";
void myfree(struct trie_node_st * rt)
{
for(int i=0; i<TREE_WIDTH; i++){
if(rt->next[i]!=NULL){
myfree(rt->next[i]);
rt->next[i] = NULL;
}
}
free(rt);
return;
}
static int
insert (const char *word)
{
int i;
struct trie_node_st *curr, *newnode;
if (word[0]=='\0'){
return 0;
}
curr = &root;
for (i=0; ; ++i) {
if (word[i] == '\0') {
break;
}
curr->pass++;//count
if (curr->next[ word[i] ] == NULL) {
newnode = (struct trie_node_st*)malloc(sizeof(struct trie_node_st));
memset (newnode, 0, sizeof(struct trie_node_st));
curr->next[ word[i] ] = newnode;
}
curr = curr->next[ word[i] ];
}
curr->count ++;
return 0;
}
static void
printword (const char *str, int n)
{
printf ("%s\t%d\n", str, n);
}
static int
do_travel (struct trie_node_st *rootp)
{
static char worddump[WORDLENMAX+1];
static int pos=0;
int i;
if (rootp == NULL) {
return 0;
}
if (rootp->count) {
worddump[pos]='\0';
printword (worddump, rootp->count+rootp->pass);
}
for (i=0;i<TREE_WIDTH;++i) {
worddump[pos++]=i;
do_travel (rootp->next[i]);
pos--;
}
return 0;
}
int
main (void)
{
char *linebuf=NULL, *line, *word;
size_t bufsize=0;
int ret;
while (1) {
ret=getline (&linebuf, &bufsize, stdin);
if (ret==-1) {
break;
}
line=linebuf;
while (1) {
word = strsep (&line, spaces);
if (word==NULL) {
break;
}
if (word[0]=='\0') {
continue;
}
insert (word);
}
}
do_travel (&root);
free (linebuf);
for(int i=0; i<TREE_WIDTH; i++){
if(root.next[i]!=NULL){
myfree(root.next[i]);
}
}
exit (0);
}
参考资料
- Black, Paul E. . Dictionary of Algorithms and Data Structures. 国家标准技术研究所. 2009-11-16 [2012-07-08]. (原始内容存档于2010-05-19).
- Franklin Mark Liang. (PDF) (Doctor of Philosophy论文). Stanford University. 1983 [2010-03-28]. (原始内容 (PDF)存档于2010-05-19).
- Knuth, Donald. . 2nd. Addison-Wesley. 1997: 492. ISBN 0-201-89685-0.
- 米嘉. (硕士论文). [2005].
- . [2012-07-19]. (原始内容存档于2009-03-19).
