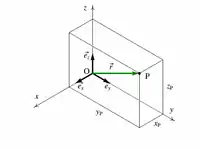
位置向量
在三维空间裏,相对于某参考点,一个质点的位置,可以用位置向量来表示。設定一坐标系,參考这坐标系,质点的坐标,就是相对于這坐标系的原点的位置向量。在运动学裏,位置向量是描述质点运动的基本参量,是一个向量:有大小,也有方向。
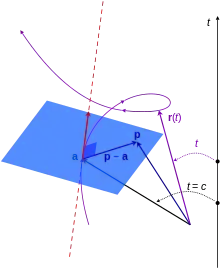
在三维空间中的曲线。位置向量r由标量t来参数化。在r = a时红色直线是这个曲线在此点的切线,垂直于蓝色平面。
位置矢量
从坐标原点指向质点所在位置的矢量称为位置矢量。
选定参考系,质点的位置由原点到质点的位置向量表示,随著时间的演化,位置向量可以描述质点的运动。在力学裏,位置向量常被用来跟踪质点、粒子、或刚体的运动。
位置向量的导数
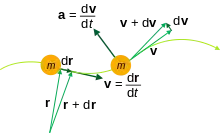
经典质点的运动学量:质量 m,位置 r,速度 v,加速度 a。
位置向量的改变称为位移,就是质点移动后的位置向量减去移动前的位置向量。位置向量對於时间的的导数称为速度:
位置向量對於时间的二阶导数称为加速度:
參閱
- 仿射空間
- 曲線
- 參數曲面()
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.