凸多胞形

在幾何學中，凸多胞形是一種點集為n維實空間凸集的幾何結構，為多胞形中的一種特例[1]。許多文獻不會明確地區分凸多胞形和凸多面體兩個術語，通常會替換地使用；而亦有一些文獻傾向於區分凸多胞形和凸多面體兩個概念。

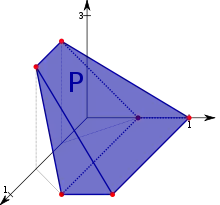
三維空間中的凸多胞形，即凸多面體。

此外部分文獻要求凸多胞形是一個有界集合[2]，亦有文獻探討的凸多胞形並不要求滿足有界集合的特性，本文探討的凸多胞形並不要求滿足有界集合的特性，而在一些較嚴謹的文獻中會用有界凸多胞形和無界凸多胞形來區分兩者的概念[3]。亦有部分的研究將n維凸多胞形是唯一個超曲面或(n-1)-流形。[4]

定義

凸多胞形的定義根據其用途和要解決的問題之不同有多種定義。例如Grünbaum對凸多胞形的定義是利用空間中的凸點集來定義的[1]

種類

凸多面體

在幾何學中，凸多面體是一種簡單多面體，其不存在邊或面自我相交的情況，且任兩點之間連成的直線皆位於多面體內部，這個特性與内部為凸集的簡單多面體等價[5]。

參見

參考文獻
  1. Branko Grünbaum, Convex Polytopes, 2nd edition, prepared by Volker Kaibel, Victor Klee, and Günter M. Ziegler, 2003, ISBN 0-387-40409-0, ISBN 978-0-387-40409-7, 466pp.
  2. Mathematical Programming, by Melvyn W. Jeter (1986) ISBN 0-8247-7478-7, p. 68
  3. Yang, Hwai-nien. . 國立政治大學學報. 1986-05, 53: 1–24.
  4. Baralic, Djordje and Milenkovic, Lazar. . arXiv preprint arXiv:1704.05932. 2017.
  5. . [2020-03-03]. （原始内容存档于2017-10-17）.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.