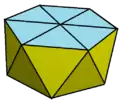
十九面體

十八角錐

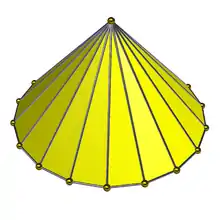十八角錐是一種底面為十八邊形的錐體，其具有19個面、36條邊和19個頂點，其對偶多面體是自己本身。正十八角錐是一種底面為正十八邊形的十八角錐。

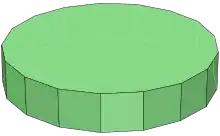十七角柱是一種底面為十七邊形的柱體，由19個面51條邊和34個頂點組成。正十七角柱代表每個面都是正多邊形的十七角柱，其每個頂點都是2個正方形和1個十七邊形的公共頂點，因此具有每個角等角的性質，可以歸類為半正十九面體，不過他跟其他較接近球形的半正多面體相比之下變得比較扁一些。

九角錐柱是指底面為九邊形的角錐柱，由19個面、32條邊和19個頂點組成，是一種十九面體。其對偶多面體為九角錐台錐，由於拓樸結構與九角錐柱相同，因此有時會被視作自身對偶多面體。

九角錐台錐是指由九角錐台和九角錐組合成的多面體，其有兩種形式：一種是九角錐疊在九角錐台較小的九邊形面、另一種是九角錐疊在九角錐台較大的九邊形面。後者可以視為只截去一個頂點的雙九角錐。

九角錐台錐的拓樸結構與九角錐柱相同，因為九角錐柱可以藉由縮放其九邊形面使圖形變形成九角錐台錐。

十七角錐台一種底面為時七邊形的錐台，可以視為切去一個頂點的十七角錐。通常其兩個底面形狀會有差異或者相似，而兩個底面都全等的十七角錐台與十七角柱無異，因此十七角錐台的拓樸結構與十七角柱相同，因為十七角柱可以藉由縮放其十七邊形面使圖形變形成十七角錐台。

六角錐反角柱是指底面為六邊形的角錐反角柱，可以視為一個六角錐與一個反六角柱底面對底面的組合。

六角錐反角柱不是一個詹森多面體，因為當其所有面都是正多邊形時，其中六個正三角形將會共面，而導致圖形退化成反六角柱。

相同的情形也出現在雙六角錐反角柱上，必須要將部分正多邊形面拉長或扭曲才能構成多面體，導致其無法以所有面皆為正多邊形的形式存在，因此這些多面體可以被歸類為擬詹森多面體[9]。

有些多面體具有19個頂點，因此其對偶多面體為十九面體。例如空間填充十三面體具有19個頂點，因此其對偶多面體是一個十九面體。

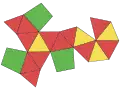
空間填充十三面體的對偶多面體是一種19面體，其可以視為一種經過扭稜變換的結果，其對應的原像與半立方體類似，但又不相同，其對應的原像有面積為零的退化面。

這個多面體一共有19個面、30條邊和13個頂點，其面由16個三角形和3個梯形所組成。其對偶多面體可以獨立填滿整個三維空間。