多面形
在幾何學中,多面形(英語:)是一種由月牙形或球弓形組成的球面鑲嵌,並且使得每一個月牙形或球弓形共用相同的兩個頂點。其在施萊夫利符號中用 {2, n} 表示n面形。
| 多面形 | |
|---|---|
 以六面形為例 | |
| 類別 | 正多面體 球面鑲嵌 |
| 面 | n |
| 邊 | n |
| 頂點 | 2 |
| 歐拉特徵數 | F=n, E=n, V=2 (χ=2) |
| 面的種類 | n個二角形 |
| 頂點圖 | 2n |
| 頂點佈局 | 2n |
| 考克斯特符號 | |
| 施萊夫利符號 | {2,n} |
| 威佐夫符號 | 2 2 |
| 對稱群 | Dnh, [2,n], (*22n), order 4n |
| 對偶 | 多邊形二面體 |
| 旋轉對稱群 | Dn, [2,n]+, (22n), order 2n |
 多邊形二面體 (對偶多面體) | |
其亦可以視為由球面正二角形組成的球面鑲嵌圖,又稱為二角形鑲嵌或二邊形鑲嵌。
正多面形
在施萊夫利符號中以{m, n}表示的正多面體,其面的個數存在下列等式:
自古以來大家所熟知的正多面體——柏拉圖立體是當m≥3且n≥3的整數解,限制在m≥3的狀態下,多邊形面必須至少有三條邊。
當考慮多面體為球面鑲嵌時,該限制可以放寬,因為二角形(二邊形)可以以球弓形或月牙形存在,即球面二角形具有非零面積。當m=2時則會產生一個新的無窮集合,即多面形。在球面上,所述多面體{2, n}表示當n個球弓形組合,並且具有2π/n內角。所有二角形階共用相同的兩個頂點,即每個頂點皆為所有二角形的公共頂點。
每個正多面形都是n階二邊形鑲嵌。
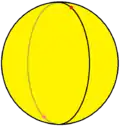
 一個正三面形,{2,3},以三個月牙形鑲嵌於求面表示。又稱三階二邊形鑲嵌。 |
 一個正四面形,以四個月牙形鑲嵌於求面表示。又稱四階二邊形鑲嵌。 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ... |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
{2,1} |
{2,2} |
{2,3} |
{2,4} |
{2,5} |
{2,6} |
{2,7} |
{2,8} |
{2,9} |
{2,10} |
{2,11} |
{2,12} | |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
多維面形
多維面形是多面形在高維度的類比,表示有多個維面的幾何圖形。任何正的維面形都可以以施萊夫利符號{2,p,...,q}表示
| 施萊夫利 {2,p,q} |
考克斯特符号 |
胞 {2,p}π/q |
面 {2}π/p,π/q |
邊 | 頂點 | 頂點圖 {p,q} |
對稱性 | 對偶多胞形 |
|---|---|---|---|---|---|---|---|---|
| {2,3,3} | 4 {2,3}π/3  |
6 {2}π/3,π/3 |
4 | 2 | {3,3} |
[2,3,3] | {3,3,2} | |
| {2,4,3} | 6 {2,4}π/3 |
12 {2}π/4,π/3 |
8 | 2 | {4,3} |
[2,4,3] | {3,4,2} | |
| {2,3,4} | 8 {2,3}π/4  |
12 {2}π/3,π/4 |
6 | 2 | {3,4} |
[2,4,3] | {4,3,2} | |
| {2,5,3} | 12 {2,5}π/3  |
30 {2}π/5,π/3 |
20 | 2 | {5,3}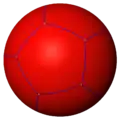 |
[2,5,3] | {3,5,2} | |
| {2,3,5} | 20 {2,3}π/5  |
30 {2}π/3,π/5 |
12 | 2 | {3,5} |
[2,5,3] | {5,3,2} |
參考文獻
- Coxeter, H.S.M; Regular Polytopes (third edition). Dover Publications Inc. ISBN 0-486-61480-8
- 埃里克·韦斯坦因. . MathWorld.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
