太阳日
太陽日(英語:)是依據太陽運動,所定義的時間,可以分為視太陽日和平太陽日。
一太阳日傳統称為一“日”、一“天”或一“昼夜”。
視太陽日
視太陽日(英語:)是依據真太阳定義的,也就是真實的太陽連續兩次經過某地相同之中天,即是上至上中天或下至下中天的時間間隔,可以使用日晷來測量(上中天)。
由於以下兩個原因,視太陽日在一年當中的長度會每天不停地改變。
- 首先,地球的軌道是一個橢圓而不是正圓,所以當地球接近太陽時速度會加快,到達近日点時的運動速度最快;遠離時又會減慢,到達远日点時的速度最慢(參考)。
- 其次,因為地球自轉軸的傾斜角度,使得太陽在黃道上運行的大圓對地球的天球赤道是傾斜的,當太陽在兩個分點時,穿越赤道時會有一個角度的,所以投影在赤道上的運行速度小於平均速度;當太陽在至點時,他的運動方向是平行於赤道的,所以投影的運行速度高於平均的速度(參考回归年)。因此,視太陽日在3月(26-27日)和9月(12-13日)是比在6月(18-19日)或12月(20-21日)短的。這些日期的長短變化是在分點、至點、遠日點、和近日點之間逐漸變化的。
| 日期 | 平太阳日 |
|---|---|
| 2月11日 | 24小时 |
| 3月26日 | 24小时 − 18.1秒 |
| 5月14日 | 24小时 |
| 6月19日 | 24小时 + 13.1秒 |
| 7月25/26日 | 24小时 |
| 9月16日 | 24小时 − 21.3秒 |
| 11月2/3日 | 24小时 |
| 12月22日 | 24小时 + 29.9秒 |
平太陽日
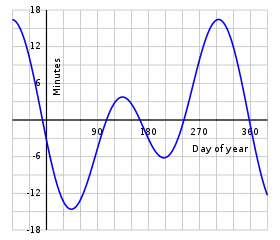
平太陽日(英語:)是以平太陽為參考點,以平太陽連續兩次經過某地之下中天的時間間隔,需花24小時來轉360°59'。更明確的說,平太陽日是經由觀察太陽相對於恆星的周日運動,所獲得的平均太陽時,經由人為的調整而顯示在時鐘上的時間。
平太陽日的長度是固定的24小時,在一年之中不會因為晝夜長短的變化而改變。視太陽日的長度會與平太陽日(86,400秒)不同,相鄰的每一天最多可以短22秒或長29秒。因為這種延長或縮短會持續進行一段時間,所以最多會比平太陽日提早17分鐘或延遲14分鐘。因為這些期間是週期性的,平太陽時和視太陽時的差值就是均時差。
在歷史上有許多方法被用來模擬(顯示)平太陽時,最早是使用漏壺或水鐘,差不多從前4000年到前2000年中期。在紀元前一千年中葉之前,水鐘只能依據視太陽日來調整,因此除了能在夜晚繼續使用外,它的準確度並不會比依靠太陽投影的日晷好。
不過,太陽相對於恆星始終是在黃道上向東移動,因此從紀元前一千年中期,相對於恆星的週日運動可以用來測量平太陽日,來比較以確定時鐘的誤差率。巴比倫的天文學家已經知道均時差和如何利用相對於恆星的自轉速率,恆星時,來改正,以獲得比水鐘更為準確的時間。這種理想的恆星時日後也應用在行星、月球和太陽運動的描述。
在20世紀初期,機械時鐘的準確度還沒有比地球自轉所顯示的恆星時鐘來得準確,即使到了今天,原子鐘的精度已經比地球的自轉更為穩定,恆星時鐘仍然被用來校準平太陽日。在20世紀末期,地球自轉的速率被改以外星系的無線電源來定義,並且平太陽時也被轉換成外來的無線電源的比率。平太陽時與协调世界时之間的差異,就成為是否需要做閏秒調整的依據。
參考
- Jean Meeus (1997), Mathematical astronomy morsels (Richmond, VA: Willmann-Bell) 346. ISBN 0-943396-51-4.
.png.webp)
