孤波

孤波是一类由于非线性作用引起的横波，它在运动过程中形状保持不变[1]。其初等函数的解析表示最早于1895年获得，并随着量子力学、电子计算机等科学技术的发展逐步受到重视。

在实验室中造波水槽里水的孤波（Solitary wave）。
钟型孤立子
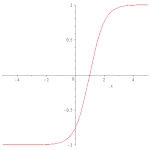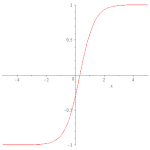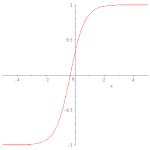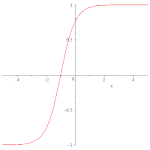
扭型孤立子
呼吸子
加德纳方程孤波
库普-库珀施密特方程孤波

孤波（英語：）又称孤子波、孤立子、孤立波，是非线性科学三大分支之一，应用于物理、数学等诸多领域。

历史

苏格兰科学家、造船工程师約翰·史考特·羅素（1808–1882）于1834年8月在英国格拉斯哥运河旁骑马时发现了自然界中的孤波——水面上滚动的水柱以每小时8-9英里[2] 的速度向前滚动，持续超过一英里。10年后，他在英国科学促进协会第14届会议上，发表论文《论水波》也称为罗素水波。

数学模型

孤波解是一类特殊的非线性偏微分方程的行波解。KdV方程、mKdV方程、非線性薛定谔方程式、Sine-Gordon方程[3] 和高次Boer-Kraup系统[4] 都有孤波解。

分类

孤波有如下几种类型：钟型孤波、反钟形孤波、扭型孤波、反扭型孤波，呼吸子等[5]。

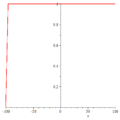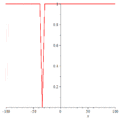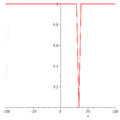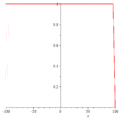  • 暗孤立子
  • 双孤立子
  • 震动孤立子

孤子按照形状和相位的角度可以分为亮孤子和暗孤子，暗孤子又可以分为黑孤子和灰孤子。亮孤子的波峰向上，相位是一个常数。而暗孤子有一个下凹的峰，在最底部的相位有π角度的突变，而灰孤子的幅值相对较小，且相位连续变化。另外还新发现了只能存在于周期系统的能隙亮孤子。

根据产生时抵消平衡的是衍射还是色散，光学中的孤子分为两类，时间孤子和空间孤子。非线性效应与色散效应导致平衡时，形成时间孤子。空间孤子的形成是由于自聚焦效应导致的光束紧缩与衍射作用下的光束扩散相抵消造成的。

其它常见分类

  • 根据横向维数不同，可以分为一维孤子和二维孤子。
  • 根据介质中有无耗散，可以分为耗散孤子和无耗散孤子。
  • 根据孤子的分量数目的不同，可以分为矢量孤子和标量孤子。矢量孤子由多个分量组成，保持稳定需要多个分量组成，而标量孤子不需要。
  • 根据孤子解的阶数，分为高阶孤子（higher-order solitons）和基本孤子（fundamental solitons）。
  • 由于介质非线性折射率不同，可以分为克尔型孤子和饱和型孤子，克尔型孤子所在介质的非线性折射率与光强强度成正比，而饱和型非线性折射率随着光强强度增加趋于饱和。

应用

孤波应用于从量子力学到光信息传输到蛋白质和DNA结构等诸多领域。

光学

光学中，单一光波束称为孤波。理论上传输稳定，不失真，被实验於光纤通信领域。

光孤立子(光孤子)，是一種脈衝，當色散被非線性效應抵銷時則此脈衝將傳輸一段距離而不會失真。

参见
維基教科書中的相關電子：孤立子

参考文献
  1. 《力学学报》（Acta Mechanica Sinica），1982年03期《应力孤子波》STRESS SOLITON WAVE，王润文上海光机所
  2. 1英里=1609.344米
  3. 阎振亚著 《复杂非线性波的构造性理论及其应用》29页 科学出版社 2007年
  4. Yu Rui Darboux Transformation and New Soliton-like Solutions
  5. 阎振亚著 《复杂非线性波的构造性理论及其应用》28页 科学出版社 2007年

A. Sergyeyev, New integrable (3+1)-dimensional systems and contact geometry, Lett. Math. Phys. 108 (2018), no. 2, 359-376, arXiv:1401.2122 doi:10.1007/s11005-017-1013-4

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.