布朗运动
布朗运动(Brownian motion)是微小粒子或者颗粒在流体中做的无规则运动。布朗运动过程是一种正态分布的独立增量连续随机过程。它是随机分析中基本概念之一。其基本性质为:布朗运动W(t)是期望为0、方差为t(时间)的正态随机变量。对于任意的r小于等于s,W(t)-W(s)独立于的W(r),且是期望为0、方差为t-s的正态随机变量。可以证明布朗运动是马尔可夫过程、鞅过程和伊藤过程。


它是在西元1827年[1]英國植物學家罗伯特·布朗利用一般的顯微鏡觀察懸浮於水中由花粉所迸裂出之微粒時,發現微粒會呈現不規則狀的運動,因而稱它布朗運動。布朗運動也能測量原子的大小,因為就是由水中的水分子對微粒的碰撞產生的,而不規則的碰撞越明顯,就是原子越大,因此根據布朗運動,定義原子的直徑為10-8厘米。
定義
自1860年以來,許多科學家都在研究此種現象,後來發現布朗運動有下列的主要特性:[2]
- 粒子的運動由平移及轉移所構成,顯得非常沒規則而且其軌跡幾乎是處處沒有切線。
- 粒子之移動顯然互不相關,甚至於當粒子互相接近至比其直徑小的距離時也是如此。
- 粒子越小或液體粘性越低或溫度越高時,粒子的運動越活潑。
- 粒子的成分及密度對其運動沒有影響。
- 粒子的運動永不停止。
對於布朗運動之誤解
值得注意的是,布朗运动指的是花粉迸出的微粒的随机运动,而不是分子的随机运动。但是通过布朗运动的现象可以间接证明分子的无规则运动。
一般而言,花粉之直徑分布於30~50μm、最小亦有10μm之譜,相較之下,水分子直徑約0.3nm(非球形,故依部位而有些許差異。),略為花粉的十萬分之一。因此,花粉難以產生不規則振動,事實上花粉幾乎不受布朗運動之影響。在罗伯特·布朗的手稿中,「tiny particles from the pollen grains of flowers」意味著「自花粉粒中迸出之微粒子」,而非指花粉本身。然而在翻譯為諸國語言時,時常受到誤解,以為是「水中的花粉受布朗運動而呈現不規則運動」。積非成是之下,在大眾一般觀念中,此誤會已然根深蒂固。

在日本,以鶴田憲次『物理学叢話』為濫觴,岩波書店『岩波理科辞典』[3]、花輪重雄『物理学読本』、湯川秀樹『素粒子』、坂田昌一『物理学原論(上)』、平凡社『理科辞典』、福岡伸一著『生物與無生物之間』,甚至日本的理科課本等等,皆呈現錯誤之敘述。
直到1973年横浜市立大学名誉教授植物学者岩波洋造在著書『植物之SEX‐不為人知的性之世界』中,點出此誤謬之前,鮮少有人注意。国立教育研究所物理研究室長板倉聖宣在參與製作岩波電影『迴動粒子』(1970年)時,實際攝影漂浮在水中之花粉,卻發現花粉完全沒有布朗運動。遂於1975年3月,以「外行人與專家之間」為題,解說有關布朗運動之誤會。
愛因斯坦的理論
在1905年,爱因斯坦提出了相关理论。他的理論有兩個部分:第一部分定義布朗粒子擴散方程式,其中的擴散係數與布朗粒子平均平方位移相關,而第二部分連結擴散係數與可測量的物理量。以此方式,愛因斯坦的理論可決定原子的大小,一莫耳有多少原子,或氣體的克分子量。根據阿伏伽德罗定律,所有理想氣體在標準溫度和壓力下體積為22.414升,其中包含的原子的數目被稱為「阿伏伽德罗常数」。由氣體的莫耳質量除以阿伏伽德罗常数等同原子量。
爱因斯坦论证的第一部分是,确定布朗粒子在一定的时间内运动的距离。[4] 经典力学无法确定这个距离,因为布朗粒子将会受到大量的撞击,每秒大约发生 1014 次撞击。[5] 因此,爱因斯坦将之简化,即讨论一个布朗粒子团的运动。
他把粒子在一个的空间中,把布朗粒子在一维方向上的运动增量 (x) 视作一个随机值( 或者 x,并对其坐标进行变换,让原点成为粒子运动的初始位置)并给出概率密度函数 。另外,他假设粒子的数量有限,并扩大了密度(单位体积内粒子数量),展开成泰勒级数 。
第一行中的第二个等式是被 这个函数定义的。第一项中的积分等于一个由概率定义函数,第二项和其他偶数项(即第一项和其他奇数项)由于空间对称性而消失。化简可以得到以下关系关系:
拉普拉斯算子之前的系数,是下一刻的随机位移量 ,让 D 为质量扩散系数:
那么在 t 时刻 x 处的布朗粒子密度 ρ 满足扩散方程:
假設在初始時刻t = 0時,所有的粒子從原點開始運動,擴散方程的解
数学模型
其他定义
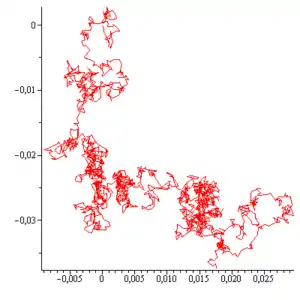
一维的定义
一维布朗运动是关于时间t的一个随机过程,他满足 :
- (独立增量)设时间t和s满足t > s,增量独立于时间s前的过程。
- (稳定增量和正态性)设时间t和s满足t > s,增量服从均值为0方差为t−s的正态分布。
- 几乎处处连续, 也就是说在任何可能性下, 函数是连续的.
- 通常假设。这种布朗运动我们称它为标准的。
等价定义
一维布朗运动是关于时间t的一个随机过程,他满足 :
高维定义
是d维布朗运动,只需满足为独立的布朗运动。
换句话说,d维布朗运动 取值于,而它在空间上的投影均为布朗运动。
Wiener测度的定义
设为从到的连续函数空间,为概率空间。布朗运动为映射
- .
Wiener测度 (或称为布朗运动的分布)设为,是映射B关于的图测度。
换句话说, W是上的一个概率测度,满足对于任何,有
- 。
备忘
- 布朗运动是一种增量服从正态分布的萊維過程。
- 这个定义可以帮助我们证明布朗运动的很多特性,比如几乎处处连续,轨迹几乎处处不可微等等。
- 我们可以利用二次变差的期望为时间来等价定义布朗运动。这个定义由Levy定理演化而来, 即: 轨迹连续且二次变差为的随机过程为布朗运动。
性质
- 布朗运动的轨道几乎处处不可微:对于任何,轨道为一个连续但是零可微的函数。
- 协方差。
- 布朗运动具有强马氏性: 对于停时T,取条件,过程为一个独立于的布朗运动。
- 它的Fourier变换或特征函数为。可见,布朗运动是一个无偏,无跳跃,二项系数为1/2的Levy过程。
- 布朗运动关于时间是齐次的: 对于s > 0, 是一个独立于的布朗运动。
- -B是一个布朗运动。
- (稳定性) 对于c > 0, 是布朗运动。
- (时间可逆性)在t=0之外是布朗运动。
- (常返性)只有1维和2维布朗运动是常返的:
- 如果,集合不是有界的,对于任何,
- 如果(几乎处处)。
- (反射原理)
利用Kolmogorov一致性定理
设为空间中一列实值函数。设:
这列函数满足:
,任意的,矩阵为对称半正定的。
利用Kolmogorov一致性定理,我们可以构造高斯过程,它的均值任意, 协方差为上面定义的。
当,为不依赖于t的常数,为上的示性函数。则:
在这个情况下,矩阵是对称且正定的。
我们称一个高斯过程为 布朗运动当且仅当均值为0,协方差为s。,当时, 称之为 标准的布朗运动.
利用随机过程
Donsker定理(1951)证明了逐渐归一化的随机游走弱收敛于布朗运动。
其中(Un, n ≥ 1) 独立同分布, 均值为0,方差为σ的随机变量序列。
利用傅立叶级数
设2列独立的正态随机变量序列和。定义:
为布朗运动。
