能量均分定理
在经典統計力學中,能量均分定理(Equipartition Theorem)是一種聯繫系統溫度及其平均能量的基本公式。能量均分定理又被稱作能量均分定律、能量均分原理、能量均分,或僅稱均分。能量均分的初始概念是熱平衡時能量被等量分到各種形式的运动中;例如,一个分子在平移運動时的平均動能應等於其做旋轉運動时的平均動能。
能量均分定理能够作出定量預測。类似于均功定理,对于一个给定温度的系统,利用均分定理,可以計算出系統的總平均動能及勢能,從而得出系统的熱容。均分定理還能分別給出能量各個组分的平均值,如某特定粒子的動能又或是一个彈簧的勢能。例如,它預測出在熱平衡時理想氣體中的每個粒子平均動能皆為(3/2)kBT,其中kB為玻爾兹曼常數而T為溫度。更普遍地,無論多複雜也好,它都能被應用於任何处于熱平衡的经典系統中。能量均分定理可用於推導经典理想氣體定律,以及固體比熱的杜隆-珀蒂定律。它亦能夠應用於預測恒星的性質,因为即使考虑相對論效應的影響,该定理依然成立。
儘管均分定理在一定条件下能够对物理现象提供非常準確的預測,但是當量子效應變得显著時(如在足够低的温度条件下),基于这一定理的预测就变得不准确。具体来说,当熱能kBT比特定自由度下的量子能級間隔要小的時候,該自由度下的平均能量及熱容比均分定理預測的值要小。当熱能比能級間隔小得多时,这样的一個自由度就說成是被“凍結”了。比方說,在低溫時很多種類的運動都被凍結,因此固體在低溫時的熱容會下降,而不像均分定理原測的一般保持恒定。對十九世紀的物理學家而言,這种熱容下降现象是表明經典物理学不再正確,而需要新的物理学的第一個徵兆。均分定理在預測電磁波的失敗(被稱为“紫外災變”)导致普朗克提出了光本身被量子化而成為光子,而這一革命性的理論對刺激量子力學及量子場論的發展起到了重要作用。
基本概念及簡易例子
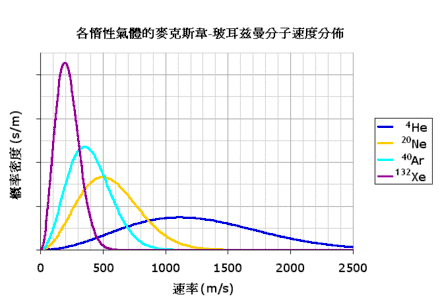
应用波尔兹曼统计方法可以得到:气体处于平衡态时,分子任何一个自由度的平均能量都相等,均为kT/2,这就是能量按自由度均分定理,简称能量均分定理。名字裏面的“均分”是指“攤分或類似於攤分”。能量均分定理的原始概念是,當系統達到熱平衡時,系統的總動能由各獨立分量所等分。均分定理也為這些能量做出量化的預測。例如它預測惰性氣體的每一個原子,當於溫度T達至熱平衡時,會有平移平均動能(3/2)KBT,其中KB為波茲曼常數。隨此引出的是,在等溫時氙的重原子速度會比氦的較輕原子要低。圖二顯示的是四種惰性氣體原子速度的麦克斯韦-玻尔兹曼分布。
在這例子中,關鍵點是動能是速度的二次齐函数。均分定理顯示出於熱平衡時,任何在能量中只以二次出現的自由度(例如是一粒子的位置或速度的一個分量)有着等於½KBT的平均能量,並因此向系統的熱容提供了½KB。這個結果有着許多的應用。
平移能量與理想氣體
一粒子質量為m,速度為v,其(牛頓力學)動能為:
其中vx、vy及vz是速度v的直角坐標的分量。這裏,H是哈密頓量,由於哈密頓表述是均分定理一般形式的中心,故下文將以其作為能量的符號。
由於能量是速度各分量的二次方,均分這三分量得每分量在熱平衡時向平均動能提供½kBT。因此粒子的平均動能為(3/2)kBT,跟上面惰性氣體的例子一樣。
更普遍地,理想氣體中的,總能量幾乎全為(平移)動能:假定粒子無內自由度且運動不受其他粒子影響。均分因此預測有N個粒子的理想氣體有平均總能量(3/2) N kBT。
而氣體的熱容則為(3/2) N kB,因此這樣一摩爾氣體的熱容為(3/2)NAkB=(3/2)R,其中NA是阿伏伽德罗常數,而R則是氣體常數。由於R ≈ 2 Cal/(mol·K),均分預測理想氣體的摩爾比熱容約為3 Cal/(mol·K)。這個預測已被實驗證實[1]。
從平均動能可以求出氣體粒子的均方根速度vrms:
其中M = NAm是一摩爾氣體粒子的質量。這個結果對很多應用方面都有用處,例如逸散用的格銳目定律為鈾濃縮提供了一個方法[2]。
旋轉能量與溶液中的分子滾翻
在另一個相近的例子中,有一粒子其主轉動慣量I1、I2及I3。它的旋轉能量是:
其中ω1、ω2及ω3是角速度的主分量。使用跟平移同一套的論證,均分意味着每個粒子的平均旋轉能量為(3/2)KBT。同樣地,均分使計算出分子均方根角速度成為可能[3]。
剛性粒子的滾翻——即是分子於溶液中的隨機旋轉——在核磁共振中觀測到弛緩中有着重要的角色,尤其是在蛋白質核磁共振及剩餘雙極耦合中[4]。旋轉滲透可被其他生物物理探測法所觀測到,例如是螢光異向性、流動雙折射及介電質光譜學[5]。
勢能與諧波振蕩器
均分定理除可應用於動能外,還能被應用於勢能計算:重要例子包括像彈簧這樣的諧波振蕩器,其二次勢能為
其中常數a描述彈簧的韌性,而q則是由平衡導出的。假若這樣一個系統的質量為m,那麼它的動能Hkin為½mv2=p2/2m,其中v及p=mv代表振蕩器的速度和動量。聯合這些項可得總能量[6]:
因此均分定理預測在熱平衡時,振蕩器有平均能量
其中角括號代表括號內的平均量[7] 。
這個結果對任何種類的諧波振蕩器都是有效的,例如鐘擺,一個振動中的粒子或是被動的電子振蕩器。這樣的振蕩器在很多情況下都會出現;由均分可得,每個這樣的振蕩器都得到一個平均總能量kBT並因此向系統熱容提供kB。這個可以被用於導出熱雜音的公式[8] 及固體摩爾比熱容的杜隆-珀蒂定律公式。後者在均分定理的歷史中尤其重要。
固體的比熱容
均分定理的一個重要應用是在於晶狀固體的比熱容。如此固體的每一個原子都能夠在三個獨立的方向下振蕩,因此該固體可以被視為一個擁有各自獨立的3N個簡諧振子的系統,其中N為晶格中的原子數。由於每一個諧振子都有平均能量kBT,所以固體的平均總能量為3NkBT,而比熱容則為3NkB。如取N為阿伏伽德罗常數NA,並使用R = NAkB這個聯繫氣體常數R及波茲曼常數kB的關係式,可得固體摩爾比熱容的杜隆-珀蒂定律的一個解釋,定律指出晶格中每摩爾的原子熱容為 3R ≈ 6 cal/(mol·K)。[9]
然而,由於量子效應的關係,這條定律在低溫時並不準確;這也不符合實驗導出的熱力學第三定律,第三定律指出摩爾比熱容於絕對零度時必為零[8]。艾爾伯特·愛因斯坦(1907年)及彼得·德拜(1911年)在基礎上加入了量子效應,發展出一套更準確的理論[10]。
固体中每个原子的振动不是独立的,可以用一組組的耦合振子作為模型。如此振蕩子的模型可以被分解成简振模,這跟鋼琴弦的振動模態及管風琴的共振模態是相近的。[11]另一方面,均分定理被應用於這種系統時一般都會失敗,因為正常模態間是沒有能量交換的。在一個非常的情況下,模態獨立且它們的能量獨立地守恒。這個顯示出有某種的能量混合,正式叫做遍歷性,對於均分定理的成立是十分重要的。[12]
粒子的澱積
勢能並不一定跟位置成二次關係的。不過,均分定理指出若能量对自由度x是s次齐次的(對一固定實數s而言),則該部份於熱平衡時的平均能量為kBT/s。
在重力下澱積的這個延伸有一個簡單的應用。例如在啤酒裏有時見到的薄霧能由一團團會散射光的蛋白質所組成[13]。一段時間以後,這些蛋白質團因受重力影響而向下沉澱,使得近底下的部份比頂端的薄霧更多。不過,一個向相合方向作用的過程中,粒子也會向上滲透回到酒瓶的頂部。一達到平衡狀態時,就可以使用均分定理來斷定某一浮力質量mb的蛋白質團的平均位置。對一支瓶高無限的啤酒而言,重力勢能可由下式求出
其中z為蛋白質團的高度,而g則為重力加速度。由於s=1的關係,蛋白質團的平均勢能等於kBT。因此,一個浮力質量為10MDa(大體上為病毒的大小)的蛋白質團會於平衡狀態做出一股2cm高的薄霧。這樣一種往平衡的澱積由梅森-韋弗爾方程所描述[14]。
歷史
動能均分這個概念最早是在1843年,或更準確地說應是1845年,由約翰·詹姆斯·瓦塔斯頓提出的[15]。於1859年,詹姆斯·克拉克·麥克斯韋主張氣體的動熱能由線性及旋轉能量所等量攤分[16] 於1876年,路德維希·波茲曼因表明了平均能量是被一系統中各獨立分量所等分,而將原理進一步擴展[17][18]。波茲曼亦應用了均分定理去為固體比熱容的杜隆-珀蒂定律提出了一個理論解釋。
能量均分定理的歷史與摩爾比熱容的歷史是密不可分的,兩者都是在十九世紀時被研究的。於1819年,法國物理學家皮埃爾·路易斯·杜隆與阿勒克西斯·泰雷塞·珀蒂發現了所有室溫下的固體比熱容幾乎都是相等的,約為6 cal/(mol·K)[20]。他們的定律曾在多年間被用作量度原子質量的一種技巧[10],然而,後來詹姆斯·杜瓦及海因里希·夫里德里希·韋伯的研究表明杜隆-珀蒂定律只於高溫時成立[21];在低溫時或像金剛石這種異常地硬的固體,比熱還要再低一點[22]。
氣體比熱的實驗觀測也引起了對均分定理是否有效的質疑。定理預測簡單單原子氣體的摩爾比熱容應約為3 cal/(mol·K),而雙原子氣體則約為7 cal/(mol·K)。實驗驗證了預測的前者[1],但卻發現雙原子氣體的典型摩爾比熱容約為5 cal/(mol·K)[23],並於低溫時下跌到約3 cal/(mol·K)[24]。詹姆斯·克拉克·麥克斯韋於1875年指出實驗與均分定理的不合比這些數字暗示的要壞得多[25];由於原子有內部部份,熱能應該走向這些內部部分的運動,使得單原子及雙原子的比熱預測值比3 cal/(mol·K)7 cal/(mol·K)要高得多。
第三個有關的不符之處是金屬的比熱[26]。根據古典德魯德模型,金屬電子的舉止跟幾乎理想的氣體一樣,因此它們應該向(3/2)NekB的熱容,其中Ne為電子的數量。不過實驗指出電子對熱容的供給並不多:很多的金屬的摩爾比熱容與絕緣體幾乎一樣[26]。
數個說明均分失敗原因的解釋被提出了。波茲曼辯護他的均分定理推導是正確的,但就提出氣體可能因為與以太相互作用而不處於熱平衡狀態[27]。由於與實驗不符,開爾文勳爵提出均分定理的推導一定是不定確的,但卻說不出甚麼不正確[28]。反而瑞利勳爵提出一個更徹底的看法,說均分定理及實驗時系統處於熱平衡的假設這兩者都正確;為使兩者相符,他指出需要一個能為均分定理提供“從破壞性的簡單中逃走的去路”的新原理[29]。艾爾伯特·愛因斯坦就提供了這條去路,於1907年他表明了這些比熱的異數都是由量子效應引起的,尤其是固體彈性模態能量的量子化[30]。愛因斯坦用了均分定理的失敗作為需要一個新物質量子理論的論據[10]。瓦爾特·能斯特於1910年在低溫的比熱量度支持了[31]愛因斯坦的理論,並引起了物理學家們對量子理論的廣泛承認[32]。
能量均分定理的通用公式化
均分定理最通用的形式[3][7][33] 明確表示在適當的假設下(下文會討論),對一個有哈密頓能量函數H及自由度xn的物理系統而言,以下均分公式於熱平衡時對任何值的指數m及n都有效:
這裏δmn為克羅內克爾δ,當m=n時為一而其他情況為零。平均用的括號可以代表一個單系統長時間的平均,或,更多地是,相空間的系綜平均。定理內含的遍歷性假設意味着這兩個平均相符,而且都被用於複雜物理系統的內能估算。
通用均分定理在系統總能量恒定時於微正則系綜有效[7],在跟能交換能量的熱庫耦合時於正則系綜亦都有效[3][34]。通式的推導在下文。
通式與以下兩式等價
- 對所有n,
- 對所有m≠n,
若一自由度xn只作為一個二次項anxn2於哈密頓函數H中出現,則可從第一式引出
即這自由度向平均能量所提供的兩倍。因此二次能量系統的均分定理結果很容易就出來了。用一個相近的論點,將2換成s,以anxns的形式應用於能量中。
自由度xn是系統相空間的坐標,因此一般被細分成廣義位置坐標qk及廣義動量坐標pk,其中pk為qk的共軛動量。此時,1式對所有k值而言
使用哈密頓力學的方程[6],這些式子可被寫成
另外式2明確指出平均為
- 及
若j≠k則皆為零。
應用
理想氣體定律
理想氣體給能量均分定理提供一個重要應用。也為每粒子的平均動能提供了公式:
能量均分定理可被用於從古典力學中導出理想氣體定律[3]。若q=(qx,qy,qz)且p=(px,py,pz)代表氣體中一個粒子的位置向量及動量向量,而F為作用在該粒子上的淨力,則
其中第一條等式為牛頓第二定律,第二行用了哈密頓力學及均分公式。將系統中的N個粒子的所有加起來得
由牛頓第三定律及理想氣體假設得,系統的淨力是由它們的容器上的牆所施行的,而這個力可由氣體的氣壓P所求得。因此
其中'dS為沿着容器牆的無限小面積元件。由於位置向量q散度為
而散度定理表明
其中dV為容器內無限小的體積,而V則為容器的總容量。
將這些等式結合得
即馬上導出N個粒子理想氣體定律
雙原子氣體
一雙原子氣體可用被一韌度為a彈簧連接的兩質量m1及m2作為模型,稱為“剛性轉子-諧波振蕩器近似法”[19]。此系統的古典能量為
其中p1與p2為兩原子的動量,而q則為從平衡值得出的原子間距離的偏差。由於能量的每一自由度都為二次,並故此應向總平均能量提供½kBT,向熱容提供½kB。因此一有N雙原子分子的氣體的熱容被預測為7N·½kB:p1及p2各提供三個自由度,q的延伸提供第七個。由此得一摩爾無其他自由度的雙原子氣體,其比熱容應為(7/2)NAkB=(7/2)R,而因此摩爾比熱容應大概為7 cal/(mol·K)。但是雙原子氣體摩熱比熱容的典型實驗結果約為5 cal/(mol·K)[23],並於非常低溫時跌至3 cal/(mol·K)。[24] 這個均分預測與實驗摩爾熱容值的不符,不能被更複雜的分子模型所解釋,因為增加自由度只會增加預測比熱值,而不會減少[25]。這個不符是需要物質量子理論的一個關鍵證據。
極度相對性理想氣體
均分定理被用於從牛頓力學中導出古典理想氣體定律。但是相對性效應在某些系統中變得顯著,例如是白矮星及中子星[7],而此時理想氣體定律一定要被稍作修改。均分定理為導出極度相對性理想氣體提供了方便的途徑[3]。在這樣的個案中,一個單粒子的動能可由以下公式求得:
以動量分量px取H的導數得公式:
之後以同樣的方式處理分量py及pz。將三個分量全加起來得:
其中最後一條等式則是均分定理公式的結果。因此,一極度相對性理想氣體的平均總能量要比非相對性的大兩倍:當有N個粒子時,總平均能量為3 N kBT。
非理想氣體
在一理想氣體中,假設粒子只通過碰撞來相互作用。均分定理可以用於推導“非理想氣體”的能量和壓力,這氣體中的粒子也通過守恒力與其他粒子相互作用,守恒力的勢U(r)只受粒子間距離r影響[3]。要描述這個狀況,首先將注意力集中於一個粒子,之後把其餘的氣體當球狀對稱分佈看待。然後按慣例引入徑向分佈函數g(r),使得從某固定粒子於距離r找到另一粒子的概率密度等於4πr2ρ g(r),其中ρ=N/V為氣體的平均密度[36]。可得某固定粒子跟其餘氣體的互相作用平均勢能為
- 。
氣體的總平均勢能因此為,其中N是氣體中的粒子數;在加起所有粒子數目的過程中會把每個粒子算兩次,所以需要用到½這個因子。
把動能及勢能加起來,然後使用均分定理,可得能量方程
- 。
用一套相近的論證下[3],可用於導出壓力方程
- 。
非諧振器
一非諧振器(跟簡單諧波振蕩器相對)的勢能並不與延伸長度q(量度平衡點偏差的廣義位置)成二次關係。這樣的振蕩器為均分定理提供了一個可作補充的觀點[37][38]。簡單例子中用的是勢能函數,其形式為
- ,
其中C和S為任意實數。這些個案中,均分定律預測
- 。
因此,平均勢能等於kBT/s,而不像二次諧波振蕩器那樣等於kBT/2(此時s=2)。
更廣義地,一次元系統典型能量函數的有以延伸長度q表示的泰勒級數:
其中n須為非負整數式子方能成立。沒有n=1的項是因為在平衡點上並無淨力作用,所以能量第一導數為零。毋需包括n=0的項是因為在約定俗成下平衡位置的能量可訂為零。此時,均分定律預測[37]:
- 。
相比以上引述的例子,均分定理公式
並不能把平均勢能以已知常數來表示。
布朗運動
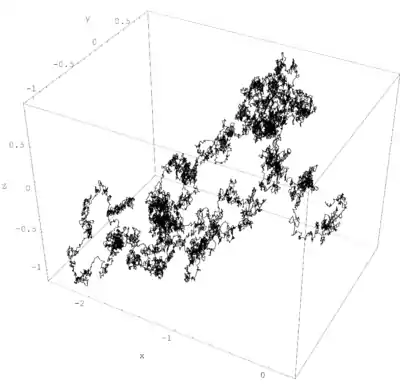
均分定理可用於從朗之萬方程中導出一粒子的布朗運動[3]。根據該方程,一質量為m,速度為v的粒子的運動是由牛頓第二定律支配的
其中Frnd為一代表着粒子及其周圍分子的隨機碰撞的隨機力,而時間常數τ反映阻礙粒子在溶液中運動的阻力。阻力很多時候被寫成Fdrag =-γv,因此時間常數τ等於m/γ。
取方程與位置向量r的點積,平均後,得布朗運動用的方程
(由於Frnd跟位置向量r不相關)。使用數學恒等式
及
布朗運動的基本方程可被轉變成
其中從最後的等式可由均分定理得平移動能:
- 。
以上的微分方程(有適當的初始條件)可被整解得
- 。
在短時標上,t <<τ,粒子的行動就像自由粒子一樣:由指數函數的泰勒級數得,距離的平方大約以二次增長:
- 。
但是在長時標上,t >>τ,對數及常數項可被忽略,距離平方只以一次增長:
- 。
這描述了粒子隨着時間的滲透。一條剛性子旋轉滲透用的類似方程可用跟這個近似的方法導出。
恒星物理學
均分定理及相關的均功定理在很早以前就已被用於天體物理學[39]。例如,均功定理可被用於由白矮星質量去估計恒星溫度或其錢德拉塞卡極限[40][41]。
一顆恒星的平均溫度可由均分定理估計[42]。由於大部份恒星都是球狀對稱,總重力勢能可由積分法估算
其中M(r)為半徑r以內的質量而ρ(r)則是於半徑r時的恒星密度;G代表萬有引力常數,R為恒星總半徑。假定整個恒星內的密度一致,該積分可得公式
其中M為恒星總質量。因此一個單粒子平均勢能為
其中N為恒星內的粒子數目。由於大部分恒星都是由離子化的氫所組成的,N大概等於(M/mp),其中mp為一個質子的質量。應用均分定理可得一個恒星溫度的約值
將太陽的質量及半徑代入得太陽溫度的大約值T等於一千四百萬開爾文,跟其核心溫度一千五百萬開爾文非常接近。但是,太陽被這個模型假設的要複雜得多——它的溫度及質量都隨半徑而變動甚大——而且如此極佳的切合度(≈7%相對誤差)在一定情況下是偶然的[43]。
推導
動能與麥克斯韋-波茲曼分布
均分定理的原公式化表述明確指出,在任何處熱平衡狀態的物理系統中,每一個粒子有着完全一樣的平均動能(3/2)kBT[46]。這可以使用麦克斯韦-玻尔兹曼分布(見圖二)表明,該分佈為對系統中一質量為m的粒子的概率分佈
- ,
麦克斯韦-玻尔兹曼分布可被用於任何物理系統,而只須假定該系統是一個正則系綜,亦即是明確地假定於溫度T時動能按波茲曼因子分佈[46]。一質量為m的粒子,可由積分式求出其平均動能
- ,
跟均分定理指出的一致。
二次能量與配分函數
更一般地說,能量均分定理明確指出任何只在總能量 中只以一簡單二次項 (此處 為一常數)出現的自由度 ,於熱平衡時有平均能量 。在這個案中均分定理可從配分函數 中導出,其中 ,為正則溫度倒數[47]。從 的式子中,經變量 取積分得因子
- ,
而跟這個因子有關的平均能量為
跟均分定理指出的一致。
一般證明
均分定理的一般證明可於很多統計力學的教科書中找到,包括微正則系綜用[3][7] 及正則系綜用[3][34] 的。它們都需要取系統相空間中的平均,而它是一個辛流形。
要解釋這些推導,需要引入以下的記法。首先,相空間是由廣義位置坐標qj跟它們的共軛動量pj一起描述的。量qj完整描述系統位形,而量(qj,pj)一起則描述完整描述系統的狀態。
第二,相空間的無限小體積
需被引入以用於定義
在這式子中,ΔE被假定為非常小的,ΔE<<E。同樣地,Σ(E)被定義為相空間中能量被E低的總體積:
由於ΔE非常小,以下這兩條積分式是等價的
其中省略号代表被積函數。由此可得Γ與ΔE成正比
此處ρ(E)為狀態密度。由統計力學常用的定義得,熵S等於kBlogΣ(E),而溫度被定義為
- 。
正則系綜
在正則系綜中,系統正與一溫度為T(以開爾文計算)的無限熱庫處與熱平衡[3][34]。在相空間中每一態的概率由波茲曼因子乘上重整化因子得出,而重整化因子的值是為使總概率成一而設的。
其中β=1/kBT。為一相空間變量xk(可為qk或pk)使用分部積分法得方程
其中dΓk=dΓ/dxk ,即第一個積分並沒有取xk積分的。第一項通常為零,這是因為在極限下xk為零,或因為能量在那極限下趨向無限。此時,可馬上得正則系綜的均分定理
這裏被符號化的平均是正則系綜中的正則平均。
微正則系綜
在微正則系綜中,系統與外界隔絕,或只是跟外界很弱的耦合起來[7]。因此,其總能量實際上是恒定的;要明確的話,則需指出總能量H局限於E及E+ΔE之間。對某固定能量E及其範圍ΔE而言,有一相空間區域Γ,在內系統有該能量且每一態在該相空間區域的機率均等。已知該等定義,相空間變量xm(可為qk或pk)的均分平均為
此處能得出最後一等式是因為E乃一常數,並不受xn影響。使用分部積分法得方程
這是由於第一行右方第一項為零的緣故(該項能被寫成在H=E的超曲面上H-E的一個積分)。
將該結果代入前面的方程可得
- 。
由於,可得均分定理
- 。
如是者就導出了均分定理的通用公式
也就是在之前應用中如此有用的那條公式。
限制
.gif)
遍歷性需求
均分定律只對處於熱平衡的遍歷系統有效,這意味着同一能量的態被遷移的可能性必然一樣[7]。故此,系統一定要可以讓它所有各形態的能量能夠互相交換,或在正則系綜中跟一熱庫一起。已被證明為遍歷的系統數量不多;雅科夫·西奈的硬球系統是一個有名的例子[48] 。讓隔離系統保證其遍歷性——因而,均分定理——的需求已被研究過,同時研究還推動了動力系統混沌理論的發展。一混沌哈密頓系統不一定是遍歷系統,儘管假定它是通常也足夠準確[49]。
有時候能量並不由它的各種形式所攤分,且此時均分定理在微正則系綜不成立,耦合諧波振蕩器系統就是在這狀況下常被引用的一個例子[49]。如果系統跟外界隔絕,那每一個正常模態的能量是恒定的;能量並不由一個模態傳遞到另一模態的。因此在這樣一個系統中均分定理無效;每一個模態能量的量都被它的起始值所固定。如果能量函數中有着足夠強的非線性量的時候,能量可能可以在正常模態中傳遞,使系統走向遍歷並使均分定律有效。然而,柯爾莫哥洛夫 - 阿諾德 - 莫澤定理明確指出除非擾動夠強,否則能量不會交換;如擾動小的話,最低限度能量會繼續受困於一些模態中。
量子效應引起的失敗
當熱能kBT比能階間的差要小得多的時候,均分法則就會失效。均分此時不再成立,是因為能階組成平滑連續能譜的這個假設跟實際情況不近似,而這假設在上面均分定理推導中有用到[3][7]。歷史上,古典均分定理在解釋比熱及黑體輻射時的失敗,對表明需要一套物質及輻射的新理論(即量子力學及量子場論)起了關鍵性的作用[10]。
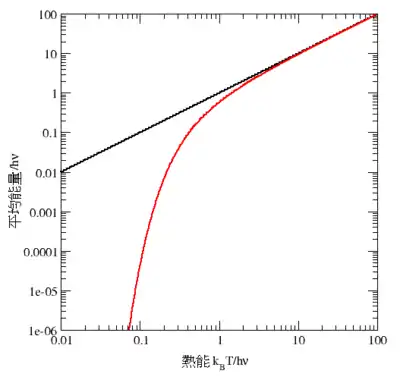
要說明均分的失效,可考慮一單(量子)諧波振蕩子的平均能量,古典個案在上文已討論過。它的量子能階為En=nhν,其中h為普朗克常數,ν為振蕩子的基本頻率,而n則為一整數。某指定能階正被置於正則系綜的概率可由其波茲曼因子得出
- ,
其中β=1/kBT,而分母中的Z為配分函數,此處為一等比級數
- 。
則其平均能量為
- 。
將Z的式子代入得最後結果[7]:
- 。
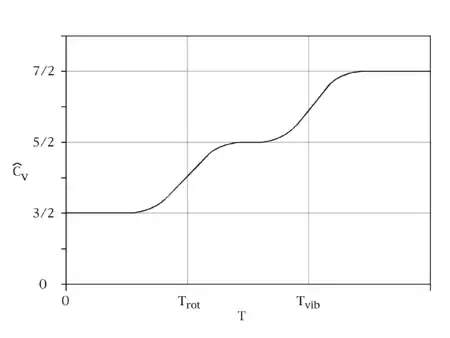
於高溫時,當熱能kBT比能階差hν大得多的時候,指數變量βhν比一要小得多,所以平均能量成了kBT,跟均分定理一致(見圖十)。然而於低溫時,當hν>>kBT的時候,平均能量走向零——高頻能階被“凍結”了(見圖十)。作為另一例子,氫原子內部的受激電子態在室溫下並不提供任何比熱,這是由於熱能kBT(大概是0.025 eV)比最低及下一高能階之間的差(大概是10 eV)要小得多的緣故。
相近的考量可用於任何能階差比熱能大得多的狀況下。例如,艾爾伯特·愛因斯坦就是用這套論證解決黑體輻射的紫外災變[50]。由於在一封閉容器下的電磁場有無限個獨立模態,每一個都能被當作諧波振蕩器看待,因而就形成了悖論。如果每一個電磁模態皆有平均能量kBT,容器內的能量將為無限大[50][51]。然而,根據以上的論證,高ω模態的平均值當ω趨向無限時趨向零;而且描術模態實驗中能量分佈的普朗克黑體輻射定律,也是根據同一組論證所中得出的[50]。
此外,更微妙的量子效應可引起均分定理的修正,例如全同粒子及連續對稱。全同粒子效應可在非常高密度且低溫時有着顯著的效果。比方說金屬的價電子可以有幾個電子伏的平均能量,正常情況一般對應數萬開爾文的溫度。如此的狀態,密度高得讓泡利不相容原理使得古典門徑無效化,被稱為簡并態費米子氣體。這種氣體對白矮星及中子星的結構很重要。在低溫時,玻色-愛因斯坦凝聚(此凝聚中大量全同粒子佔據了低能量態)的費米子類比能夠形成;這種超流體電子是引起超導現象的成因。
註釋及參考資料
- Kundt, A; Warburg E. . Annalen der Physik. 1876, 157: 353–369. (德文)
- Fact Sheet on Uranium Enrichment U.S. Nuclear Regulatory Commission. Accessed 30th April 2007
- Pathria, RK. . Pergamon Press. 1972: pp. 43–48, 73–74. ISBN 978-0-08-016747-3.
- Cavanagh, J; Fairbrother WJ, Palmer AG III, Skelton NJ, Rance M. 2nd ed. Academic Press. 2006. ISBN 978-0-12-164491-8.
- Cantor, CR; Schimmel PR. . W. H. Freeman. 1980. ISBN 978-0-7167-1189-6.
- Goldstein, H. 2nd. ed. Addison-Wesley. 1980. ISBN 978-0-201-02918-5.
- Huang, K. 2nd ed. John Wiley and Sons. 1987: pp. 136–138. ISBN 978-0-471-81518-1.
- Mandl, F. . John Wiley and Sons. 1971: pp. 213–219. ISBN 978-0-471-56658-8.
- 林宗涵. . 北京大学出版社. 2007: 290-291. ISBN 9787301106549.
- Pais, A. . Oxford University Press. 1982. ISBN 978-0-19-853907-0.
- 林宗涵. . 北京大学出版社. 2007: 293-296. ISBN 9787301106549.
- Alwyn Scott,Emeritus. . Routledge. 2006: 274. ISBN 9781135455583.
- Miedl M, Garcia M, Bamforth C. . J. Agric. Food Chem. 2005, 53 (26): 10161–5. PMID 16366710.
- Mason, M; Weaver W. . Physical Review. 1924, 23: 412–426.
- Brush, SG. . Amsterdam: North Holland. 1976: 134–159. ISBN 978-0-444-87009-4.
Brush, SG. . Amsterdam: North Holland. 1976: 336–339. ISBN 978-0-444-87009-4.
Waterston, JJ. . Roy. Soc. Proc. 1846/1893, 5: 604. (abstract only). Not published in full until Philos. Trans. R. Soc. London. 1893, A183: 1–79. 缺少或|title=为空 (帮助) Reprinted J.S. Haldane (编). . Edinburgh: Oliver & Boyd. 1928.
Waterston, JJ. . 1843. (reprinted in his Papers, 3, 167, 183.)
Waterston, JJ. British Association Reports. 1851, 21: 6. 缺少或|title=为空 (帮助)。 瓦塔斯頓的關鍵論文是於1845年向英國皇家學會提交的。在他拒絕發表他的研究後,學會也拒絕退回稿件並予以存檔。該原稿於1845年被瑞利勳爵發現,他對當時未能夠認可瓦塔斯頓研究重要性的審查員作出了批評。瓦塔斯頓成功將他的見解於1851年發表,因此比麥克斯韋宣佈第一版的能量均分定理要早 - Maxwell, JC. . WD Niven (编). . New York: Dover. 2003: Vol.1, pp. 377–409. ISBN 978-0-486-49560-6.。1859年9月21日,在英國科學促進協會在阿伯丁的一次會議中,由麥克斯韋教授讀出。
- Boltzmann, L. . Wiener Berichte. 1871, 63: 679–711. (德文) 在這一份初步研究中,波茲曼表明了當系統被外在和諧力作用時,其平均總動能等於平均總勢能。
- Boltzmann, L. . Wiener Berichte. 1876, 74: 553–560. (德文)
- McQuarrie, DA. revised 2nd ed. University Science Books. 2000: pp. 91–128. ISBN 978-1-891389-15-3.
- Petit, AT; Dulong PL. . Annales de Chimie et de Physique. 1819, 10: 395–413. (法文)
- Dewar, J. . Philosophical Magazine. 1872, 44: 461.
Weber, HF. . Annalen der Physik. 1872, 147: 311–319. (德文)
Weber, HF. . Annalen der Physik. 1875, 154: 367–423, 553–582. (德文) - de la Rive, A; Marcet F. . Annales de Chimie et de Physique. 1840, 75: 113–144. (法文)
Regnault, HV. . Annales de Chimie et de Physique. 1841,. 1 (3me Série): 129–207. (法文) 1841年1月11日於法國自然科學院被讀出。
Wigand, A. . Annalen der Physik. 1907, 22: 99–106. (德文) - Wüller, A. . Leipzig: Teubner. 1896: Vol. 2, 507ff. (德文)
- Eucken, A. . Sitzungsberichte der königlichen Preussischen Akademie der Wissenschaften. 1912, 1912: 141–151. (德文)
- Maxwell, JC. . WD Niven (编). . Cambridge: At the University Press. 1890: Vol.2, pp.418–438. ASIN B000GW7DXY.
- Kittel, C. . New York: John Wiley and Sons. 1996: 151–156. ISBN 978-0-471-11181-8.
- Boltzmann, L. . Nature. 1895, 51: 413–415.
- Thomson, W. . Baltimore: Johns Hopkins University Press. 1904: Sec. 27. Re-issued in 1987 by MIT Press as Kelvin's Baltimore Lectures and Modern Theoretical Physics: Historical and Philosophical Perspectives (Robert Kargon and Peter Achinstein, editors). ISBN 978-0-262-11117-1
- Rayleigh, JWS. . Philosophical Magazine. 1900, 49: 98–118.
- Einstein, A. . Annalen der Physik. 1907, 22: 180–190.(德文)
Einstein, A. . Annalen der Physik. 1907, 22: 800. (德文)
Einstein, A. . Annalen der Physik. 1911, 34: 170–174. (德文)
Einstein, A. . Annalen der Physik. 1911, 34: 590. (德文)
Einstein, A. . Annalen der Physik. 1911, 35: 679–694. (德文) - Nernst, W. . Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften. 1910, 1910: 262–282. (德文)
- Hermann, Armin. original title: Frühgeschichte der Quantentheorie (1899–1913), translated by Claude W. Nash. Cambridge, MA: The MIT Press. 1971: pp. 124–145. ISBN 978-0-262-08047-7, LCCN 73-0.
- Tolman, RC. . Physical Review. 1918, 11: 261–275.
- Tolman, RC. . New York: Dover Publications. 1938: pp. 93–98. ISBN 978-0-486-63896-6.
- Clausius, R. . Annalen der Physik. 1870, 141: 124–130. (德文)
Clausius, RJE. . Philosophical Magazine, Ser. 4. 1870, 40: 122–127. - McQuarrie, DA. revised 2nd ed. University Science Books. 2000: pp. 254–264. ISBN 978-1-891389-15-3.
- Tolman, RC. . Chemical Catalog Company. 1927: pp. 76–77.
- Terletskii, YP. translated: N. Fröman. Amsterdam: North-Holland. 1971: pp. 83–84. ISBN 978-0-7204-0221-6, LCCN 70-0.
- Collins, GW. . Pachart Press. 1978. 外部链接存在于
|title=(帮助) - Chandrasekhar, S. . Chicago: University of Chicago Press. 1939: pp. 49–53.
- Kourganoff, V. . Dordrecht, Holland: D. Reidel. 1980: pp. 59–60, 134–140, 181–184.
- Chiu, H-Y. . Waltham, MA: Blaisdell Publishing. 1968. LCCN 67-0 – 0.
- Noyes, RW. . Cambridge, MA: Harvard University Press. 1982. ISBN 978-0-674-85435-2.
- Ostlie, DA; Carroll BW. . Reading, MA: Addison-Wesley. 1996. ISBN 978-0-201-59880-3.
- Jeans, JH. . Phil.Trans. A. 1902, 199: 1–53.
- McQuarrie, DA. revised 2nd ed. University Science Books. 2000: pp. 121–128. ISBN 978-1-891389-15-3.
- Callen, HB. . New York: John Wiley and Sons. 1985: pp. 375–377. ISBN 978-0-471-86256-7.
- Arnold, VI; Avez A. . Gauthier-Villars, Paris. (法文) (English edition: Benjamin-Cummings, Reading, Mass. 1968). 1967.
- Reichl, LE. 2nd ed. Wiley Interscience. 1998: 326–333. ISBN 978-0-471-59520-5.
- Einstein, A. . Annalen der Physik. 1905, 17: 132–148. (德文). 英語維基文庫上有本論文的英語翻譯。
- Rayleigh, JWS. . Philosophical Magazine. 1900, 49: 539–540.
延伸閱讀
- Huang, K. 2nd ed. John Wiley and Sons. 1987: pp. 136–138. ISBN 978-0-471-81518-1.
- Khinchin, AI. . New York: Dover Publications. 1949: pp. 93–98. ISBN 978-0-486-63896-6.
- Landau, LD; Lifshitz EM. 3rd ed. Pergamon Press. 1980: pp. 129–132. ISBN 978-0-08-023039-9.
- Mandl, F. . John Wiley and Sons. 1971: pp. 213–219. ISBN 978-0-471-56658-8.
- Mohling, F. . John Wiley and Sons. 1982: pp. 137–139, 270–273, 280, 285–292. ISBN 978-0-470-27340-1.
- Pathria, RK. . Pergamon Press. 1972: pp. 43–48, 73–74. ISBN 978-0-08-016747-3.
- Pauli, W. . MIT Press. 1973: pp. 27–40. ISBN 978-0-262-16049-0.
- Tolman, RC. . Chemical Catalog Company. 1927: pp. 72–81. ASIN B00085D6OO
- Tolman, RC. . New York: Dover Publications. 1938: pp. 93–98. ISBN 978-0-486-63896-6.
外部連結
- 一單原子及雙原子混合氣體的均分定理即時Applet展示(英文)
- 恒星物理中的能量均分定理 Archived 2012-06-30 at WebCite,由耶路撒冷希伯來大學Racah物理研究所副教授Nir J. Shaviv所撰寫。(英文)