截角正五胞体
截角正五胞体由十个三维胞组成: 五个正四面体, 和五个截角四面体。每个顶点周围环绕着三个截角四面体和一个正四面体。截角正五胞体是截角四面体的四维类比。
| 截角正五胞体 | |
|---|---|
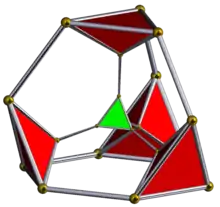 施莱格尔投影 (正四面体胞在前) | |
| 類型 | 均匀多胞体 |
| 胞 | 10 5 (3.3.3) 5 (3.6.6) |
| 面 | 30 20 {3} 10 {6} |
| 邊 | 40 |
| 頂點 | 20 |
| 顶点图 |  Irr. tetrahedron |
| 施萊夫利符號 | t0,1{3,3,3} |
| 考克斯特記號 | |
| 參考索引 | 2 3 4 |
| 考克斯特群 | A4, [3,3,3], order 120 |
| 對偶多胞體 | 四角化正五胞體 |
| 特性 | convex, isogonal |
构造
截角正五胞体的细胞可以通过在正五胞体的棱的三分点处截断其顶点。截断的五个正四面体变成新的截角四面体,并在原来的顶点处产生了五个新的正四面体。
结合
截角四面体的六边形面彼此结合在一起,而它们的三角形面则连接到正四面体。
参考文献
- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 0-486-40919-8 p.88 (Chapter 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues, Proceedings of the London Mathematics Society, Ser. 2, Vol 43, 1937.)
- Coxeter, H. S. M. Regular Skew Polyhedra in Three and Four Dimensions. Proc. London Math. Soc. 43, 33-62, 1937.
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
- Olshevsky, George, Pentachoron at Glossary for Hyperspace.
- 1. Convex uniform polychora based on the pentachoron - Model 3, George Olshevsky.
- Richard Klitzing, 4D, uniform polytopes (polychora) x3x3o3o - tip, o3x3x3o - deca
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.





