拉格朗日方程式

假設一個物理系統符合完整系統的要求，即所有廣義座標都互相獨立，則拉格朗日方程式成立：

${\displaystyle {\frac {d}{dt}}{\frac {\partial {\mathcal {L}}}{\partial {\dot {\mathbf {q} }}}}-{\frac {\partial {\mathcal {L}}}{\partial \mathbf {q} }}=\mathbf {0} \,\!}$；

其中，${\displaystyle {\mathcal {L}}(\mathbf {q} ,\ {\dot {\mathbf {q} }},\ t)\,\!}$是拉格朗日量，${\displaystyle \mathbf {q} =\left(q_{1},q_{2},\ldots ,q_{N}\right)\,\!}$是廣義座標，是時間${\displaystyle t\,\!}$的函數，${\displaystyle {\dot {\mathbf {q} }}=\left({\dot {q}}_{1},{\dot {q}}_{2},\ldots ,{\dot {q}}_{N}\right)\,\!}$是廣義速度。

在分析力學裏，有三種方法可以導引出拉格朗日方程式。最原始的方法是使用達朗貝爾原理導引出拉格朗日方程式（參閱達朗貝爾原理）；更進階層面，可以從哈密頓原理推導出拉格朗日方程式（參閱哈密頓原理）；最簡明地，可以借用數學變分法的歐拉-拉格朗日方程式來推導：

設定函數${\displaystyle \mathbf {y} (x)\,\!}$和${\displaystyle f(\mathbf {y} ,\ {\dot {\mathbf {y} }},\ x)\,\!}$：

${\displaystyle \mathbf {y} (x)=(y_{1}(x),\ y_{2}(x),\ \ldots ,y_{N}(x))\,\!}$、

${\displaystyle {\dot {\mathbf {y} }}(x)=({\dot {y}}_{1}(x),\ {\dot {y}}_{2}(x),\ \ldots ,\ {\dot {y}}_{N}(x))\,\!}$、

${\displaystyle f(\mathbf {y} ,\ {\dot {\mathbf {y} }},\ x)=f(y_{1}(x),\ y_{2}(x),\ \ldots ,\ y_{N}(x),\ {\dot {y}}_{1}(x),\ {\dot {y}}_{2}(x),\ \ldots ,\ {\dot {y}}_{N}(x),\ x)\,\!}$；

其中，${\displaystyle x\,\!}$是自變數（）。

若${\displaystyle \mathbf {y} (x)\in (C^{1}[a,\ b])^{N}\,\!}$使泛函${\displaystyle J(\mathbf {y} )=\int _{a}^{b}f(\mathbf {y} ,\ {\dot {\mathbf {y} }},\ x)dx\,\!}$取得局部平穩值，則在區間${\displaystyle (a,\ b)\,\!}$內，歐拉-拉格朗日方程式成立：

${\displaystyle {\frac {d}{dx}}\left({\frac {\partial }{\partial {\dot {y}}_{i}}}f(\mathbf {y} ,\ {\dot {\mathbf {y} }},\ x)\right)-{\frac {\partial }{\partial y_{i}}}f(\mathbf {y} ,\ {\dot {\mathbf {y} }},\ x)=0\ ,\qquad \qquad \qquad \qquad i=1,\ 2,\ \ldots ,\ N\!}$。

現在，執行下述轉換：

• 設定獨立變數${\displaystyle x\,\!}$為時間${\displaystyle t\,\!}$、
• 設定函數${\displaystyle y_{i}\,\!}$為廣義坐標${\displaystyle q_{i}\,\!}$、
• 設定泛函${\displaystyle f(\mathbf {y} ,\ {\dot {\mathbf {y} }},\ x)\,\!}$為拉格朗日量${\displaystyle {\mathcal {L}}(\mathbf {q} ,\ {\dot {\mathbf {q} }},\ t)\,\!}$，

則可得到拉格朗日方程式

${\displaystyle {\frac {d}{dt}}{\frac {\partial {\mathcal {L}}}{\partial {\dot {\mathbf {q} }}}}-{\frac {\partial {\mathcal {L}}}{\partial \mathbf {q} }}=\mathbf {0} \,\!}$。

• 為了滿足這轉換的正確性，廣義坐標必須互相獨立，所以，這系統必須是完整系統。
• 拉格朗日量是動能減去位勢，而位勢必須是廣義位勢。所以，這系統必須是單演系統。

主項目：參閱半完整系統

一個不是完整系統的物理系統是非完整系統，不能用上述形式論來分析。假若，一個非完整系統的約束可以以方程式表示為

${\displaystyle g_{i}(\mathbf {q} ,\ {\dot {\mathbf {q} }})=0\ ,\qquad \qquad \qquad i=1,\ 2,\ 3,\ \dots n\,\!}$；

則稱此系統為半完整系統[1]。

半完整系統可以用拉格朗日形式論來分析。更具體地說，分析半完整系統必須用到拉格朗日乘子${\displaystyle \lambda _{i}\,\!}$：

${\displaystyle \sum _{i=1}^{n}\ \lambda _{i}g_{i}=0\,\!}$；

其中，${\displaystyle \lambda _{i}=\lambda _{i}(\mathbf {q} ,\ {\dot {\mathbf {q} }},\ t)\,\!}$是未知函數。

由於這${\displaystyle N\,\!}$個廣義坐標中，有${\displaystyle n\,\!}$個相依的廣義坐標，泛函${\displaystyle f(\mathbf {y} ,\ {\dot {\mathbf {y} }},\ x)\,\!}$不能直接被轉換為拉格朗日量${\displaystyle {\mathcal {L}}\,\!}$；必須加入拉格朗日乘子，將泛函${\displaystyle f(\mathbf {y} ,\ {\dot {\mathbf {y} }},\ x)\,\!}$轉換為${\displaystyle {\mathcal {L}}+\sum _{i=1}^{n}\ \lambda _{i}g_{i}\,\!}$。這樣，可以得到拉格朗日廣義力方程式：

${\displaystyle {\frac {d}{dt}}{\frac {\partial {\mathcal {L}}}{\partial {\dot {\mathbf {q} }}}}-{\frac {\partial {\mathcal {L}}}{\partial \mathbf {q} }}={\boldsymbol {\mathcal {F}}}\,\!}$；

其中，${\displaystyle {\boldsymbol {\mathcal {F}}}\,\!}$是廣義力，${\displaystyle {\boldsymbol {\mathcal {F}}}={\frac {\partial }{\partial \mathbf {q} }}\left(\sum _{i=1}^{n}\ \lambda _{i}g_{i}\right)-{\frac {d}{dt}}\left[{\frac {\partial }{\partial {\dot {\mathbf {q} }}}}\left(\sum _{i=1}^{n}\ \lambda _{i}g_{i}\right)\right]\,\!}$。

這${\displaystyle N\,\!}$個廣義力運動方程式加上${\displaystyle n\,\!}$個約束方程式，給出${\displaystyle N+n\,\!}$個方程式來解${\displaystyle N\,\!}$個未知廣義坐標與${\displaystyle n\,\!}$個拉格朗日乘子。

這個段落會展示拉格朗日方程式的兩個應用實例。第一個實例展示出，用牛頓方法與拉格朗日方法所得的答案相同。第二個實例展示出拉格朗日方法的威力，因為這問題比較不適合用牛頓方法來分析。

具有質量的移動支撐點的簡單擺

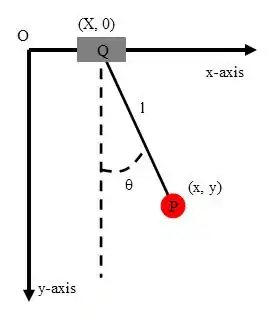
思考一個簡單擺系統。系統的x-軸平行於地面，y-軸垂直於x-軸，指向地面。擺錘P的質量是${\displaystyle m\,\!}$，位置是${\displaystyle (x,\ y)\,\!}$。擺繩的長度是${\displaystyle l\,\!}$。擺的支撐點Q的質量是${\displaystyle M\,\!}$。這支撐點Q可以沿著一條平行於x-軸的直線移動。點Q的位置是${\displaystyle (X,\ 0)\,\!}$。擺繩與y-軸的夾角是${\displaystyle \theta \,\!}$。那麼，動能是

${\displaystyle T={\frac {1}{2}}M{\dot {X}}^{2}+{\frac {1}{2}}m\left({\dot {x}}^{2}+{\dot {y}}^{2}\right)\,\!}$，

位勢為

${\displaystyle V=-mgy\,\!}$。

所以，拉格朗日量是

${\displaystyle {\mathcal {L}}={\frac {1}{2}}M{\dot {X}}^{2}+{\frac {1}{2}}m\left({\dot {x}}^{2}+{\dot {y}}^{2}\right)+mgy\,\!}$。

兩個約束方程式為

${\displaystyle x=X+l\sin \theta \,\!}$、

${\displaystyle y=l\cos \theta \,\!}$。

將約束方程式代入拉格朗日量方程式,

${\displaystyle {\mathcal {L}}={\frac {1}{2}}M{\dot {X}}^{2}+{\frac {1}{2}}m\left[\left({\dot {X}}+l{\dot {\theta }}\cos \theta \right)^{2}+\left(l{\dot {\theta }}\sin \theta \right)^{2}\right]+mgl\cos \theta \,\!}$。

特別注意，在這裏，廣義坐標是${\displaystyle X\,\!}$與${\displaystyle \theta \,\!}$。應用拉格朗日方程式，經過微分運算，對於${\displaystyle X\,\!}$坐標，可以得到

${\displaystyle {\frac {d}{dt}}\left[(M+m){\dot {X}}+ml{\dot {\theta }}\cos \theta \right]=0\,\!}$。

運動方程式為

${\displaystyle (M+m){\ddot {X}}+ml{\ddot {\theta }}\cos \theta -ml{\dot {\theta }}^{2}\sin \theta =0\,\!}$。

由於拉格朗日量不顯含廣義坐標${\displaystyle X\,\!}$，稱${\displaystyle X\,\!}$為可略坐標，而其相對應的廣義動量${\displaystyle p_{X}\,\!}$是常數${\displaystyle K_{1}\,\!}$：

${\displaystyle p_{X}=(M+m){\dot {X}}+ml{\dot {\theta }}\cos \theta =K_{1}\,\!}$。

對於${\displaystyle \theta \,\!}$坐標，可以得到

${\displaystyle {\frac {d}{dt}}\left[m(l^{2}{\dot {\theta }}+{\dot {X}}l\cos \theta )\right]+m({\dot {X}}l{\dot {\theta }}+gl)\sin \theta =0\,\!}$；

所以，運動方程式為

${\displaystyle {\ddot {\theta }}+{\frac {\ddot {X}}{l}}\cos \theta +{\frac {g}{l}}\sin \theta =0\,\!}$。

假如用牛頓第二定律，則必須仔細地辨明所有的相關作用力。這是一項既困難又容易出錯的工作。

• 拉格朗日量
• 拉格朗日力學
• 哈密頓力學
• 牛頓力學
• 變分法