控制流圖

控制流圖（control-flow graph）簡稱CFG，是计算机科学中的表示法，利用數學中图的表示方式，標示计算机程序執行過程中所經過的所有路徑。控制流圖是由法兰·艾伦所建立[1]，他提出Reese T. Prosser曾利用邻接矩阵用在流分析上[2]。

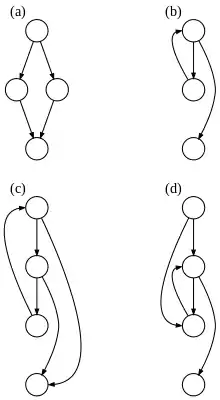
  此條目介紹的是表示程式中控制流的有向圖。关于商業流程建模的流程圖，请见「控制流程圖」。
一些S控制流圖的例子：
(a)if-then-else
(b)while迴圈
(c)有二個離開點的自然迴圈，例如：在中間有break指令的while迴圈，非結構化，但是reducible
(d)irreducible的CFG：有二個進入點的迴圈，例如用goto進入for迴圈或while迴圈內

CFG是許多編譯器最佳化及靜態程序分析工具中的核心技術。

定義

控制流圖中的每個顶点都對應一個程式基本塊，也就是一段沒有分支指令，也沒有分支目的的程式碼，基本塊的開始是分支目的，而基本塊會以分支為結束。控制流程中會用有向邊來表示分支。在大部份的進行下，會有二個特殊指定的程式塊：進入程式塊（entry block）是指進入此控制流圖時，第一個遇到的程式碼，另一個是結束程式塊（exit block）是所有流程在結束時都會執行的程式碼[3]。

因為控制流圖的生成方式，在控制流圖中，每一個有向邊A→B會有以下的性質：

outdegree(A) > 1 或 indegree(B) > 1（也可能同時成立）[4]。

以概念上來看，控制流圖可以由程式的完整流程圖產生。先畫出一個控制流圖，其中每一個頂點對應程式中的一個指令。接著對每一個邊進行边收缩，將不符合上述條件的邊（就是outdegree(A) = 1 且 indegree(B) = 1的邊）和相鄰的邊整合。這個收縮演算法在實務上沒有什麼重要性，但可以以視覺的方式說明控制流圖的產生方式。而實務上產生控制流圖的方式會更有效率的掃描程式中的基本塊來達成[4]。

舉例

考慮以下的程式片段：

0: (A) t0 = read_num
1: (A) if t0 mod 2 == 0
2: (B)   print t0 + " is even."
3: (B)   goto 5
4: (C) print t0 + " is odd."
5: (D) end program

以上程式中，有四個基本塊，第0行至第1行的A，第2行到第3行的B，第4行的C以及第5行的D。在此例中，A是進入程式塊，D是結束程式塊，第4行及第5行是分支目的。這段程式的控制流圖有從A到B、從A到C、從B到D、從C到D。

可到達性

可到達性是圖論中的性質，會用在程式的最佳化中。

若某一個子圖沒有和包括進入程式塊的子圖相連接，在執行程式時不會執行到該子圖的程式，因此是不可到達程式碼，在一般情形下可以移除該程式，不會影響程式運作。

若從進入程式塊無法連到結束程式塊，則可能有無窮迴圈。不過不是所有的無窮迴圈都可以檢測的到（參考停机问题）。

即使程式設計者沒有刻意的寫不可到達程式碼或是無窮迴圈，仍有可能會出現這些情形。像是常數折疊或常數傳播等最佳化方式，若後面有跳转线程，可能會將數個基本塊變成一個，因此移除了控制流圖上的一些邊，也可能因此出現不可到達程式碼

支配關係
主条目：支配 (圖論)

若從進入程式塊到達基本塊N的所有路徑，都會在到達基本塊N之前先到達基本塊M，則基本塊M支配（dominates）基本塊N。進入程式塊支配自身之外，所有的基本塊。

考慮相反的方向，若基本塊N到達結束程式塊的所有路徑，都會在結束程式塊之前先到達基本塊M，則基本塊M後置支配（postdominates）基本塊N。結束程式塊後置支配自身之外，所有的基本塊。

若基本塊M支配基本塊N，且其中間沒有任何基本塊P，使得基本塊M支配基本塊P，且基本塊P支配基本塊N，則基本塊M直接支配（immediately dominates）基本塊N，也就是說，基本塊M是基本塊N的直接支配者中，最靠近基本塊N的一個。每一個基本塊都有唯一的直接支配者。

同樣的，也有直接後置支配者（immediate postdominator）的概念。

支配樹（dominator tree）是描述支配關係的輔助資料結構。若M直接支配N，基本塊M到基本塊N就會有弧線。因為每一個基本塊都只有一個直接支配者，因此所形成的會是樹。可以用Lengauer-Tarjan算法快速的計算支配樹。

同樣的，也可以繪製後置支配樹（postdominator tree）。

特殊邊

倒退邊（back edge）是指向的基本塊是在圖的深度优先搜索中，已經走過的基本塊。倒退邊多半表示有迴圈。

異常邊（abnormal edge）是目的不清的邊。建構异常处理時常會產生這種邊。此情形會不允許最佳化。

不可能邊（impossible edge）也稱為假邊（fake edge），是為了讓結束程式塊後置支配所有節點而加入的邊，其實不會執行到。

迴圈管理

迴圈首標（loop header）也稱為迴圈的進入點。是指一個支配基本塊，同時也是倒退邊的目標。循環首標是迴圈中其他基本塊的支配者。基本塊也可能是多個迴圈的迴圈首標。若迴圈有多個進入點，就沒有迴圈首標。

假設基本塊M是有數個進入點的支配基本塊，其中有些是倒退邊（因此M是迴圈首標）,有一個有利於許多最佳化程序的作法，是將基本塊M分為基本塊Mpre和基本塊Mloop。基本塊M的內容以及倒退邊移到Mloop，其餘的移到Mpre，建立一個從Mpre到Mloop的邊（因此Mpre是Mloop的直接支配者。一開始時，Mpre可能是空的，但在經過循環不變代碼運動，Mpre就會慢慢增加。Mpre稱為迴圈前首標（loop pre-header），而Mloop為新的迴圈首標。

可规约性

可规约控制流圖（reducible CFG）是指邊可以分為前進邊及倒退邊二個不交集，因此[5]：

  • 前進邊會形成有向无环图，其中所有的節點都是可到達的節點。
  • 針對所有倒退邊（A, B），節點B支配節點A。

结构化编程程式語言常會設計讓產生的所有控制流圖都是可规约控制流圖，常見的流程控制指令 (例如IF、FOR、WHILE、BREAK、CONTINUE）都會產生可规约控制流圖。若要讓控制流圖不可规约，需要加上Goto之類的指令。在一些編譯器的最佳化過程中，可能會出現不可规约控制流圖。

迴圈連結度

控制流圖的迴圈連結度（loop connectedness）是以控制流圖的給定深度优先搜索樹（DFST）為準。DFST需以啟始節點為根，包括控制流圖中的所有節點。

若控制流圖中的邊，是從一個節點到DFST中的祖先節點，此邊為倒退邊。

迴圈連結度是指控制流圖中沒有迴圈的路徑中，可以找到倒退邊的最大數量。若是可规约控制流圖，迴圈連結度和選擇的DFST無關[6][7]。

迴圈連結度可以用來說明数据流分析的時間複雜度[6]。

相關條目

參考資料
  1. Frances E. Allen. . SIGPLAN Notices. July 1970, 5 (7): 1–19. doi:10.1145/390013.808479.
  2. Reese T. Prosser. . 1959: 133–138.
  3. Yousefi, Javad. . IEEE: 201–205. 2015. doi:10.1109/ICCKE.2015.7365827.
  4. Peri L. Tarr; Alexander L. Wolf. . Springer Science & Business Media. 2011: 58. ISBN 978-3-642-19823-6.
  5. http://www.cs.colostate.edu/~mstrout/CS553Fall06/slides/lecture13-control.pdf
  6. Kam, John B.; Ullman, Jeffrey D. . Journal of the ACM. 1976-01-01, 23 (1): 158–171. ISSN 0004-5411. doi:10.1145/321921.321938.
  7. Offner, Carl. (PDF). [13 April 2018].

外部連結
维基共享资源中相关的多媒体资源：控制流圖
例子
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.