有向无环图

有向无环图的可达性可以用其顶点的偏序关系≤来表示。在偏序关系中，如果存在一条路径从顶点u指向顶点v，它们的偏序关系可被写作u ≤ v。这也被称作v是从u可达的。[6]不同的有向无环图可以有着相同的可达关系和偏序关系。[7]例如，有两条边a → b，b → c的有向无环图，和有三条边的a → b, b → c，a → c的有向无环图有着相同的偏序关系a ≤ b ≤ c。

对于一个有向无环图G，它的传递闭包等同于一个在保持与其相同可达性的情况下，边数最多的图。在这个图中，当u可达v的时候，边u → v必定存在。换句话说，每个G中的非相同元素偏序关系对u ≤ v都在这个图中有一条边。这可以被视作用图来可视化图G的可达性关系。

有向无环图G

G的传递规约

有向无环图G的传递规约为和其有着相同可达性，边数最少的图。它是G的一个子图。构造方法为当G有着一条更长的路径连接顶点u和v的时候，消去边u → v。 传递约简和传递闭包都是有向无环图的特有概念。相反的，对于有向有环图，可以存在多个与原图有着相同可达性的最简子图。[8]

将{ x, y, z }的幂集按包含偏序排序得到的哈斯图

对于有向无环图G和表达其可达性的偏序关系≤，它的传递规约也可以看作包含G的覆盖关系中每一条边的G的子图。传递规约在图示有向无环图的偏序关系时十分有用，因为它们比其他具有相同偏序关系的图的边数要少，这简化了绘图。偏序关系的哈斯图由将传递规约中的每条边的起点绘制在其终点的下方而得到。[9]

有向无环图的拓扑排序为所有边的起点都出现在其终点之前的排序。能构成拓扑排序的图一定没有环，因为环中的一条边必定从排序较后的顶点指向比其排序更前的顶点。[3]基于此，拓扑排序可以被用来定义有向无环图：当且仅当一个有向图有拓扑排序，它是有向无环图。一般情况下，拓扑排序并非唯一。有向无环图仅仅在存在一条路径可以包含其所有顶点的情况下，有唯一的拓扑排序方式，这时，拓扑排序与它们在这条路径中出现的顺序相同。[10]

有向无环图的拓扑排序族等同于其可达性的线性拓展族。 [11]因此，偏序关系相同的任意两个图会有相同的拓扑排序集。

罗宾逊 (1973)研究了有向无环图的图计数问题。[12] 如标号顶点在拓扑排序中出现的顺序不受限制，有n个顶点的标号有向无环图的数量为

1, 1, 3, 25, 543, 29281, 3781503, … （OEIS中的数列A003024）。

其中n = 0, 1, 2, 3,……。这个数列的递推关系式是

${\displaystyle a_{n}=\sum _{k=1}^{n}(-1)^{k-1}{n \choose k}2^{k(n-k)}a_{n-k}.}$[12]

埃里克·韦斯坦因推测[13]，n个顶点的标号有向无环图的数量与其中所有特征值都为正实数的n*n逻辑矩阵的数量相同。这一点随后被证实，证明采用了双射法：一个矩阵A是有向无环图的一个邻接矩阵，当且仅当A + I是一个所有特征值都为正数的逻辑矩阵，其中I为单位矩阵。因为一个有向无环图不允许自环，它的邻接矩阵的对角线必定全为0。因此，加上I保持了所有矩阵因子都是0或1的特性。[14]

一颗多重树

强明确树

多重树由将自由树的边定向而得到。[15] 多重树必定是有向无环图。对于有根树，将其所有边赋予指离根的方向也可以得到有向无环图，即树状图。

强明确树是每两个顶点最多被一条路径所连接的有向无环图。等价的说，它是满足以下性质的一个有向无环图：对于图中每个顶点v，从v可达的顶点组成一颗树。[16]

可以用线性时间复杂度的卡恩算法来找到一个有向无环图的拓扑排序。[17]简单来说，开设一个存放结果的列表L，先将入度为零的节点放到L中，因为这些节点没有任何的父节点。将与这些节点相连的边从图中去掉，再寻找图中入度为零的节点。对于新找到的节点来说，他们的父节点已经都在L中了，所以也可以从末端插入L。重复上述操作，直到找不到入度为零的节点。[18] 另外一种构造拓扑排序的算法是将深度优先搜索的后序遍历结果翻转。[17]

检查一个有向图是否为有向无环图亦可在线性时间内完成。一种方法是先找到一个拓扑排序，然后测试这个排序是否能符合图中每条边所连顶点在排序中应该出现的顺序。[19] 对于卡恩算法在内的部分拓扑排序算法，通过在算法终止时判断是否满足一定条件即可知道图是否有环。[18]如果有环，卡恩算法最终获得的L中节点个数会与图的节点总数不同。

任意无向图都可以被转化为有向无环图。构造方法是选定一个顶点的全序关系，并将无向图中所有边从全序关系中较前的顶点指向较后的顶点。这种方法是定向方法中的无环定向。不同的全序关系可能推出相同的无环定向，因此一个包含n个顶点的图的无环定向数量小于n!。如果定义χ为给定图的色多项式，无环定向数量等于|χ(−1)|。[20]

任意有环有向图都可以被转化为有向无环图。只要从图中移除反馈节点集或反馈边集，即对于图中每个环，至少包括环中一个顶点或边的集合。不过，找到反馈节点或边的最小集合是NP困难问题。[21] 另外一种方法将有环有向图去环的方法是将每个强连通分量收缩为一个顶点。[22] 对于无环图，它的最小反馈顶点或边集为空集，它的强连通分量则为自身。

有向无环图的传递闭包可以通过广度优先搜索或深度优先搜索对每个节点测试可达性来构建。算法对于一个有着n个顶点和m条边的有向无环图的复杂度为O(mn)。[23]也可以使用矩阵乘法算法中最快的Coppersmith–Winograd算法，其复杂度为O(n^2.3728639)。这个算法理论上在稠密图中快过O(mn)。[24]

不论在哪种传递闭包算法中，那些被一条长度至少为2的路径所连接的顶点对，都可以和只有一条长度为1的路径所连接的顶点对区分开。由于传递约简包含后者，传递约简可以在和传递闭包相同的渐进时间复杂度中被构建。[25]

闭包是一个图中没有出边的顶点子集，即不存在从子集中顶点指向子集外顶点的边。闭包问题是则是找到带权图中使得权之和最大或最小的子集。闭包问题可以看作最大流问题的简化版，在多项式时间内被解决。实际上，是否有环对于找到闭包没有影响。[26]

基于拓扑排序的性质，有向无环图的最短路问题和最长路径问题可以在线性时间内解决。将顶点拓扑排序后，从前到后遍历每一个顶点，对于遍历到的顶点，更新其所有出边所到达顶点的长度值。如果求最短路，则在本边是更短路径的一部分时更新。求最长路则反之。[27]对于非有向无环图，最短路需要用复杂度为${\displaystyle O(|E|+|V|\log |V|)}$的戴克斯特拉算法或${\displaystyle O(|V||E|)}$的贝尔曼-福特算法等。[28]最长路径则是一个NP困难问题。[29]

有向无环图的偏序关系可以在调度有着先后顺序限制的系统任务中发挥作用。[30]调度问题的一个重要种类是串联需要更新的对象，如電子試算表中某个单元格的计算公式依赖于其他单元格，或在程序的源代码被修改后重新编译目标文件。依赖图则记录了这种更新依赖关系。其每个顶点对应一个需要被更新的对象，边则表示更新的关系。依赖图中的环被称为环状依赖。环状依赖通常是不被允许出现的，因为不能保证圈内任务排定顺序的一致性。无环的依赖图即为有向无环图。[31]

举例来说，当电子表格中一个单元格的数值发生改变，其他直接或间接依赖于该单元格的所有单元格的值都需要被重新计算。被调度的任务为重新计算某个特定单元格的值。当一个单元格的值取决于另外一个单元格时，两个单元格之间则有依赖关系。每个被依赖单元格的值的计算过程都必须先于使用它的表达式执行。使用依赖图的拓扑排序来调度任务使得在每个单元格的值都仅被重新计算一次的情况下，整个工作表都能被更新。[32]相似的任务调度场景出现在程序源代码编译的makefile，[32]和优化计算机程序底层执行的指令调度中.[33]

一个有着五个里程碑（注有10–50）和六个任务（注有A–F）的计划评审图。ADF和BC是关键路径

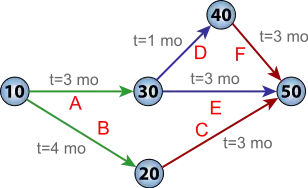
计划评审技术是一种基于有向无环图的计划排定技术，通常用于组织大型的人工项目。在计划评审技术中，每个顶点表示项目的一个里程碑，每条有向边表示任务或者活动，连接着表示任务开始或结束的两个节点。每条边则被标注上预估需时。图中的最长路径即为项目的关键路径。关键路径决定了项目所需的总时间，里程碑的完成时间取决于结束于本顶点的最长路径。[34]

有向无环图可以用于表示处理数据的元素网络。在网络中，数据从一个元素顶点的入边进入，处理后从出边离开。

在电子电路设计中，静态组合逻辑电路块可以被表示为由邏輯閘组成的有向无环系统。每个逻辑门对输入做一次函数处理，输入和输出均为一个位元组。通常，这些电路块的输出不能够再作为输入，除非它们被存储在寄存器或者状态单元中，以保证图不出现环。[35]

数据式编程语言描述针对数据流的操作，以及操作的输出和其他操作的输入之间的关系。这类型的语言使得描绘高重复率数据处理任务的变得更加简单，因为同样的数据操作可以应用于许多数据项。数据操作可以用有向无环图来表示。这些数据操作可以被并发执行，从而高效利用多核心处理器。[36]

在編譯器中，直线码（不含条件分支和循环的代码段）可以使用有向无环图表示。图标示出每个算术运算的输入和输出。这种表示法让编译器能执行通用子表达式删除，使得代码更高效。[37]

用顶点表示事件，边表示因果关系的图通常是无环的。[38]事件由时间上的先后顺序来排列，所有箭头遵循从先发生事件指向后发生事件的原则，因此也不存在环。

举例来说，貝氏網路表示多个概率事件的关联网络。顶点表示事件，后续事件的发生可能性则可以通过其在有向无环图的前驱节点的发生概率计算出来。[39]在此基础上，一个有向无环图的端正图通过以下方法而得到：将单个顶点的所有父节点之间添加一条无向边，再将所有的有向边换成无向边。[40]

另外一种具有相似因果结构的图是影响图。其顶点表示决策或不确定的事件，边表示两个顶点之间的因果关系。[41]在流行病学中，这些表示因果关系的图表常常用来评估不同干预手段的效果。[42][43]

托勒密王朝的谱系图。

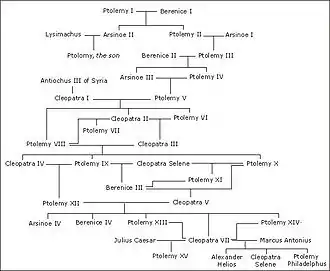
谱系图可以看作是有向无环图，顶点代表家族成员，边代表亲子关系。[44]虽然谱系图也被称作为家族“树”, 但近亲结婚导致的血统崩溃会违反树的性质。即一个孩子的祖先既可以从父亲向上追溯，也可以从母亲一侧。[45]图中的母系血统和父系血统则可以看作为树。因为没有人可以是自己的祖先，谱系图是无环的。[46]

基于相同的原因， 一个分散式版本控制系统的版本历史的结构也是有向无环图。在系统中，每个版本对应一个节点。边连接起有直接衍生关系的两个版本。由于分支合并的存在，这个结构并不能用树来表示。[47]

在计算几何领域，许多随机化算法都会维护一个“历史有向无环图”，用以记录结构变动中的旧几何结构。例如，在德勞內三角化的随机增量算法中，在添加每个点时，通过用三个较小的三角形替换一个三角形，以及通过“翻转”操作将三角形对替换为另一对三角形，来改变三角剖分。在该算法的历史有向无环图中，每个在算法中构建出的三角形对应一个顶点，边则将每个三角形和替代它的两个或三个三角形连接起来。这种图结构可以高效地处理点定位问题，即对于一个查询点q，找到它在德勞內三角剖分中的位置。在历史有向无环图中，从起点开始，不断移动到包含q的替代三角形组，最后到达的终点必定代表包含q的德劳内三角形。[48]

在引用图中， 每个顶点代表单篇著作，边代表著作之间的引用关系。1965年普莱斯的文章“科学文献的网络”是使用引用图的一个经典例子。[49]在引用图中，每篇论文的引用次数为对应顶点的入度。这是引文分析中的一种重要的展示方式。另一个例子是法律裁判中，法官通过引用过往案例中的判决来支持他们的结论。引用图亦可以用来描绘专利，因为专利必须要提及现有技术，即已经公开的并且和本专利有关的先前专利。

相较于网络科学中对一般图的研究，有向无环图的独特性质可以被用来作深层次分析。例如，传递规约可以呈现引用在不同应用领域的分布情况，这突出了不同领域中不同的引用网构造机制。[50]引用图的衍生概念还有主干道路分析，即对引用图中最显著的一条路径的分析。

分别用trie（左）和有向无环词图（右）存放英文单词“tap”，“taps”，“top”和“tops”。EOW表示单词结束。

有向无环图也可以用于对一系列序列的压缩中。在这里，有向无环图中的路径代表这些序列。当多个序列有共同的子序列时，子序列可以被表示为这些序列对应路径的公共边。比起直接列出所有序列，这种方法占用更少空间。例如，有向无环词图为仅含单个源（入度为0的顶点）的有向无环图，其每条边附有一个或多个字符。每条其源到汇（出度为0的节点）的路径均代表一个字符串，字符串可以是英文单词。[51]与其结构不同但功能相似的树称为trie。相比于trie，有向无环词图允许多条边指向同一个顶点，使得具有相同后缀的一些词的词头可以被相同的顶点所表示，因而更省空间。[52]

二元决策图是基于有向无环图的一种数据结构，用于表示布尔函数[53][54]。在二元决策图中，每个非汇节点对应一个布尔变量，每个汇和边则表示0或1。要找到一个解释的真值，只要从唯一的源顶点出发，沿着该顶点代表的布尔变量的实际真值所对应的出边一直前进，到达的汇则为其真值。如同有向无环词图可以被看作是trie的一种压缩形式一样，二元决策图可以被看作是决策树的压缩形式。它通过将导向相同结果的边重新汇合到一个顶点来节省空间。[55]