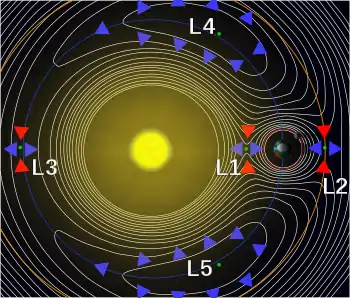
晕轮轨道

在航天动力学的三体问题中，晕轮轨道是一种靠近L1, L2或 L3 拉格朗日点周期性的三维轨道。虽然拉格朗日点只是太空中空无一物的一个点，但奇怪的是能围绕它旋转。晕轮轨道被看作是两个行星性物体的引力、科氏力和离心力互相作用于航天器的结果。晕轮轨道存在于任意一个三体系统中，如日-地系统和地-月系统。每一个拉格朗日点都同时存在北晕轮轨道和南晕轮轨道。由于晕轮轨道倾向于不稳定状态，需要轨道位置固定技术将卫星保持在轨道上。

围绕L1, L2, or L3 拉格朗日点旋转的天体的晕轮轨道（不是等比例的）

定义与历史

罗伯特·威拉德·法夸尔率先将“晕轮轨道”这一名称用于他的1968年博士论文中。[1]法夸尔支持在阿波罗任务中，在地月系统L2点使用航天器用作通讯中继站。在这样的一条晕轮轨道上的航天器将会连续地看到地球和月球的远端。最后，在阿波罗以往的月球背面登月任务中，通信中继卫星或阿波罗联合任务都没有停泊在L2[2]。

法夸尔使用解析表达式表达晕轮轨道，但凯瑟琳·豪威尔表示能用数值计算出更明确的轨迹。[3]

晕轮轨道的第一个应用的任务是1978年发射的国际彗星探测器。它行进至日地L1点，在那里逗留了数年时间。晕轮轨道应用的第二次任务是太阳和太阳圈探测器（SOHO），欧空局和美国国家航空航天局研究太阳的联合任务，1996年，它抵达日地L1点。它使用一条与国际彗星探测器相似的轨道。[4]虽然从那以后的数个其他任务曾行进到过拉格朗日点，但是它们一贯使用[5]非周期性变化的利萨如轨道，而非真实的晕轮轨道。如2001年发射的起源号探测器，该探测器是动态系统理论的应用先驱，以找到低能转移轨道的方法。

法夸尔的设想于2018年6月实现。中国航天局在2018年6月14日将鹊桥号中继卫星成功移动至地月拉格朗日L2点的晕轮轨道。[6][7][8] 2019年3月，嫦娥四号使用鹊桥中继卫星进行了软着陆，传回了月球背面的图像。[9][10]

相关条目
  • 行星间传输网络
  • 利萨如轨道，另一个拉格朗日点轨道，即一般化的晕轮轨道。

参考资料
  1. Farquhar, R. W.: "The Control and Use of Libration-Point Satellites", Ph.D. Dissertation, Dept. of Aeronautics and Astronautics, Stanford University, Stanford, California, 1968
  2. Schmid, P. E. (PDF). NASA. June 1968 [2008-07-16].
  3. Howell, K. C.: "Three-Dimensional, Periodic, 'Halo' Orbits", Celestial Mechanics, Volume 32, Number 53, 1984
  4. Dunham, D.W. and Farquhar, R. W.: "Libration-Point Missions 1978-2000," Libration Point Orbits and Applications, Parador d'Aiguablava, Girona, Spain, June 2002
  5. . www.quora.com. [2015-05-31].
  6. Jones, Andrew. . GB times. 1 June 2018 [2018-06-14]. （原始内容存档于2018-06-14） （英语）.
  7. . チャイナデイリー. 14 June 2018 [2018-06-14]. （原始内容存档于2018-06-14） （英语）.
  8. Xu, Luyuan. . The Planetary Society. 2018-06-15 [2020-05-13]. （原始内容存档于2018-10-17） （英语）. This is the first-ever lunar relay satellite at this location.
  9. Jones, Andrew. . GBTIMES. 2018-12-05 [2020-05-13]. （原始内容存档于2018-12-11）.
  10. . SpaceNews.com. 2019-01-03 [2019-01-08] （美国英语）.

外部链接
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.