浸入

數學上，浸入是微分流形之間的可微映射，其導數處處是單射。確切而言，f : M → N是浸入，若在M中每一點p，

${\displaystyle D_{p}f:T_{p}M\to T_{f(p)}N\,}$

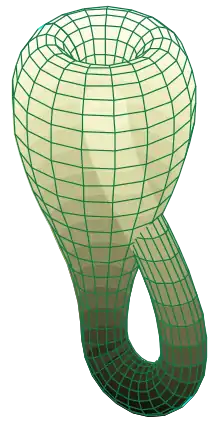
克萊因瓶浸入到3-空間中。

都是单射。（T_pX表示X在點p處的切空間。另一個等價說法是f是浸入，若f的秩是常數，且等於M的維數：

${\displaystyle \operatorname {rank} \,D_{p}f=\dim M.}$

以上只要求f的導數為單射，但映射f未必是單射。

一個與浸入相關的概念是嵌入。光滑嵌入是一個單射浸入f : M → N而同時為拓撲嵌入，使得M與其在N中的像微分同胚。浸入正是局部嵌入，即對M中每一點x都有一個x的鄰域U ⊂ M，使得f : U → N是嵌入。相反地，局部嵌入都是浸入。

一個單射浸入子流形而不是嵌入。

若M是緊緻的，則單射浸入是一個嵌入；若M不是緊緻，則未必成立。這兩者的關係就如同連續雙射之於同胚。