直接推理

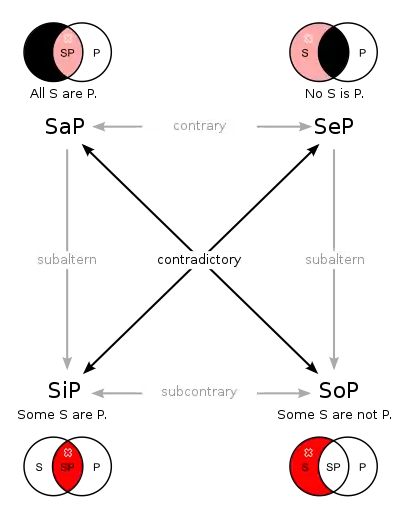
直言命题的四种类型的谓词逻辑表示：

• 全称肯定命题（A）：${\displaystyle \forall x(S(x)\rightarrow P(x))}$，所有S都是P
• 全称否定命题（E）：${\displaystyle \forall x(S(x)\rightarrow \lnot P(x))}$，所有S都不是P
• 特称肯定命题（I）：${\displaystyle \exists x(S(x)\land P(x))}$，有些S是P
• 特称否定命题（O）：${\displaystyle \exists x(S(x)\land \lnot P(x))}$，有些S不是P

依据全称量词和存在量词之间的对偶关系（对立四边形中矛盾关系）可以直接得出：

• 全称肯定命题（A）：${\displaystyle \lnot \exists x(S(x)\land \lnot P(x))}$，没有S不是P
• 全称否定命题（E）：${\displaystyle \lnot \exists x(S(x)\land P(x))}$，没有S是P
• 特称肯定命题（I）：${\displaystyle \lnot \forall x(S(x)\rightarrow \lnot P(x))}$，并非所有S都不是P
• 特称否定命题（O）：${\displaystyle \lnot \forall x(S(x)\rightarrow P(x))}$，并非所有S都是P

上面加粗表述是亞里士多德《解釋篇》中採用的形式。

假定了主词对应的范畴确有个体存在之后可得出蘊涵關係（又譯差等關係）：

• 全称肯定命题（A）蕴涵了特稱肯定命题（I）：${\displaystyle \exists xS(x)\land \forall x(S(x)\rightarrow P(x))\Rightarrow \exists x(S(x)\land P(x))}$
• 全称否定命题（E）蕴涵了特稱否定命题（O）：${\displaystyle \exists xS(x)\land \forall x(S(x)\rightarrow \lnot P(x))\Rightarrow \exists x(S(x)\land \lnot P(x))}$

在蘊涵關係和對偶關係之上可確立全稱命題間不同真關係（又譯反對關係）：

• 全称肯定命题（A）為真則全称否定命题（E）為假：${\displaystyle \exists xS(x)\land \forall x(S(x)\rightarrow P(x))\Rightarrow \lnot \forall x(S(x)\rightarrow \lnot P(x))}$
• 全称否定命题（E）為真則全称肯定命题（A）為假：${\displaystyle \exists xS(x)\land \forall x(S(x)\rightarrow \lnot P(x))\Rightarrow \lnot \forall x(S(x)\rightarrow P(x))}$

和特稱命題之間的不同假關係（又譯下反對關係）：

• 特稱肯定命題（I）為假則特稱否定命題（O）為真：${\displaystyle \exists xS(x)\land \lnot \exists x(S(x)\land P(x))\Rightarrow \exists x(S(x)\land \lnot P(x))}$
• 特稱否定命題（O）為假則特稱肯定命題（I）為真：${\displaystyle \exists xS(x)\land \lnot \exists x(S(x)\land \lnot P(x))\Rightarrow \exists x(S(x)\land P(x))}$

换位法对调主词和谓词的位置（采用谓词逻辑就没有了传统的主词谓词差别）：

• 全称肯定命题（A）蕴涵特称肯定命题（I）：${\displaystyle \exists xS(x)\land \forall x(S(x)\rightarrow P(x))\Rightarrow \exists x(P(x)\land S(x))}$，有些P是S(假定了某个S的存在)
• 全称否定命题（E）：${\displaystyle \forall x(P(x)\rightarrow \lnot S(x))}$，所有P都不是S
• 特称肯定命题（I）：${\displaystyle \exists x(P(x)\land S(x))}$，有些P是S

换质法否定谓词本身而改变命题的性质，这裡有${\displaystyle A^{CC}=A\,}$：

• 全称肯定命题（A）变为全称否定命题（E）：${\displaystyle \forall x(S(x)\rightarrow \lnot P^{C}(x))}$，所有S都不是非P
• 全称否定命题（E）变为全称肯定命题（A）：${\displaystyle \forall x(S(x)\rightarrow P^{C}(x))}$，所有S都是非P
• 特称肯定命题（I）变为特称否定命题（O）：${\displaystyle \exists x(S(x)\land \lnot P^{C}(x))}$，有些S不是非P
• 特称否定命题（O）变为特称肯定命题（I）：${\displaystyle \exists x(S(x)\land P^{C}(x))}$，有些S是非P

对置法是换质后换位：

• 全称肯定命题（A）变为全称否定命题（E）：${\displaystyle \forall x(P^{C}(x)\rightarrow \lnot S(x))}$，所有非P都不是S
• 全称否定命题（E）蕴涵特称肯定命题（I）：${\displaystyle \exists xS(x)\land \forall x(S(x)\rightarrow P^{C}(x))\Rightarrow \exists x(P^{C}(x)\land S(x))}$，有些非P是S(假定了某个S的存在)
• 特称否定命题（O）变为特称肯定命题（I）：${\displaystyle \exists x(P^{C}(x)\land S(x))}$，有些非P是S

特称肯定命题（I）变为特称否定命题（O）後不能換位。

对置后再换质叫反对置法（Obverted Contraposition）：

• 全称肯定命题（A）变为全称肯定命题（A）：${\displaystyle \forall x(P^{C}(x)\rightarrow S^{C}(x))}$，所有非P都是非S
• 全称否定命题（E）蕴涵特称否定命题（O）：${\displaystyle \exists xS(x)\land \forall x(S(x)\rightarrow P^{C}(x))\Rightarrow \exists x(P^{C}(x)\land \lnot S^{C}(x))}$，有些非P不是非S(假定了某个S的存在)
• 特称否定命题（O）变为特称否定命题（O）：${\displaystyle \exists x(P^{C}(x)\land \lnot S^{C}(x))}$，有些非P不是非S

• 集合代数
• 直言三段论
• 传统逻辑
• 解释篇