解析信号

在数学和信号处理中，解析信号（英語：）是没有负频率分量的复值函数。[1] 解析信号的实部和虚部是由希爾伯特轉換相关联的实值函数。

实值函数的解析表示是解析信号，包含原始函数和它的希尔伯特变换。这种表示促进了许多数学变换的发展。基本的想法是，由于频谱的埃尔米特对称，实值函数的傅里叶变换（或频谱）的负频率成分是多余的。若是不介意处理复值函数的话，这些负频率分量可以丢弃而不损失信息。这使得函数的特定属性更易理解，并促进了调制和解调技术的衍生，如单边带。只要操作的函数没有负频率分量（也就是它仍是“解析函数”），从复数转换回实数就只需要丢弃虚部。解析表示是相量概念的一个推广：[2] 相量限制在时不变的振幅、相位和频率，解析信号允许有时变参数。

定义

创建一个解析信号的传递函数

若 $s(t)$ 是一个实值函数，其傅里叶变换为 $S(f)$ ， $S(f)$ 為一於 $f=0$ 埃尔米特对称之函數：

S(-f)=S(f)^{*},

其中，

S(f)^{*}

为

S(f)

的复共轭。

函数：

{\begin{aligned}S_{\mathrm {a} }(f)&{\stackrel {\mathrm {def} }{{}={}}}{\begin{cases}2S(f),&{\text{for}}\ f>0,\\S(f),&{\text{for}}\ f=0,\\0,&{\text{for}}\ f<0\end{cases}}\\&=\underbrace {2\operatorname {u} (f)} _{1+\operatorname {sgn}(f)}S(f)=S(f)+\operatorname {sgn}(f)S(f),\end{aligned}}

其中：

$\operatorname {u} (f)$ 是单位阶跃函数，

$\operatorname {sgn}(f)$ 是符号函数，

仅包含 $S(f)$ 的非负频率分量。而且由于 $S(f)$ 的埃尔米特对称性，该运算是可逆的：

{\begin{aligned}S(f)&={\begin{cases}{\frac {1}{2}}S_{\mathrm {a} }(f),&{\text{for}}\ f>0,\\S_{\mathrm {a} }(f),&{\text{for}}\ f=0,\\{\frac {1}{2}}S_{\mathrm {a} }(-f)^{*},&{\text{for}}\ f<0\ {\text{(Hermitian symmetry)}}\end{cases}}\\&={\frac {1}{2}}[S_{\mathrm {a} }(f)+S_{\mathrm {a} }(-f)^{*}].\end{aligned}}

$s(t)$ 的解析信号是 $S_{\mathrm {a} }(f)$ 的傅里叶逆变换：

{\begin{aligned}s_{\mathrm {a} }(t)&{\stackrel {\mathrm {def} }{{}={}}}{\mathcal {F}}^{-1}[S_{\mathrm {a} }(f)]\\&={\mathcal {F}}^{-1}[S(f)+\operatorname {sgn}(f)\cdot S(f)]\\&=\underbrace {{\mathcal {F}}^{-1}\{S(f)\}} _{s(t)}+\overbrace {\underbrace {{\mathcal {F}}^{-1}\{\operatorname {sgn}(f)\}} _{j{\frac {1}{\pi t}}}*\underbrace {{\mathcal {F}}^{-1}\{S(f)\}} _{s(t)}} ^{convolution}\\&=s(t)+j\underbrace {\left[{1 \over \pi t}*s(t)\right]} _{\operatorname {\mathcal {H}} [s(t)]}\\&=s(t)+j{\hat {s}}(t),\end{aligned}}

其中

${\hat {s}}(t){\stackrel {\mathrm {def} }{{}={}}}\operatorname {\mathcal {H}} [s(t)]$ 是 $s(t)$ 的希爾伯特轉換；
$*$ 是卷积符号；
$j$ 是虛數單位。

例子

例1

s(t)=\cos(\omega t),

其中

\omega >0.

于是：

{\hat {s}}(t)=\cos(\omega t-\pi /2)=\sin(\omega t),

s_{\mathrm {a} }(t)=s(t)+j{\hat {s}}(t)=\cos(\omega t)+j\sin(\omega t)=e^{j\omega t}.

第三个等式为欧拉公式。

欧拉公式的一个推论是 $\cos(\omega t)={\tfrac {1}{2}}(e^{j\omega t}+e^{j(-\omega )t}).$ 一般来说，简单正弦曲线的解析表示是通过用复指数表示它，丢弃负频率分量，并对正频率分量加倍得到的。正弦曲线之和的解析表示等于单个正弦波的解析表示之和。

例2

这里我们使用欧拉公式来识别并丢弃负频率。

s(t)=\cos(\omega t+\theta )={\tfrac {1}{2}}(e^{j(\omega t+\theta )}+e^{-j(\omega t+\theta )})

于是：

s_{\mathrm {a} }(t)={\begin{cases}e^{j(\omega t+\theta )}\ \ =\ e^{j|\omega |t}\cdot e^{j\theta },&{\text{if}}\ \omega >0,\\e^{-j(\omega t+\theta )}=\ e^{j|\omega |t}\cdot e^{-j\theta },&{\text{if}}\ \omega <0.\end{cases}}

例3

这是使用希尔伯特变换方法去除负频率分量的另一个例子。我们注意到，对于复值函数 $s(t)$ ，没有什么能阻止我们计算 $s_{\mathrm {a} }(t)$ 。但它可能不是一种可逆的表示，因为原频谱不总是对称的。所以除了此例以外，一般讨论都假设 $s(t)$ 为实值函数。

s(t)=e^{-j\omega t}

, 其中

\omega >0

.

于是：

{\hat {s}}(t)=je^{-j\omega t},

s_{\mathrm {a} }(t)=e^{-j\omega t}+j^{2}e^{-j\omega t}=e^{-j\omega t}-e^{-j\omega t}=0.

负频率分量

由于 $s(t)=\operatorname {Re} [s_{\mathrm {a} }(t)]$ ，恢复负频率分量就是简简单单丢弃 $\operatorname {Im} [s_{\mathrm {a} }(t)]$ 这件事可能与直觉不太一致。我们还可以注意到复共轭 $s_{\mathrm {a} }^{*}(t)$ 仅由负频率分量构成。因此 $\operatorname {Re} [s_{\mathrm {a} }^{*}(t)]$ 恢复了被减弱的正频率分量。

应用

包络和瞬时相位

一个函数（蓝色）和它的解析表示的模（红），显示出包络现象。

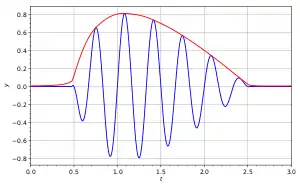
解析信号也可以表示在其随时间变化的幅度和相位（极坐标）：

s_{\mathrm {a} }(t)=s_{\mathrm {m} }(t)e^{j\phi (t)},

其中：

$s_{\mathrm {m} }(t){\stackrel {\mathrm {def} }{{}={}}}|s_{\mathrm {a} }(t)|$ 称作瞬时振幅或包络；
$\phi (t){\stackrel {\mathrm {def} }{{}={}}}\arg \!\left[s_{\mathrm {a} }(t)\right]$ 称作瞬时相位。

在附图中，蓝色曲线描绘 $s(t)$ ，红色曲线描绘对应的 $s_{\mathrm {m} }(t)$ 。

解缠的瞬时相位的时间导数的单位为rad/s，称作瞬时角频率：

\omega (t){\stackrel {\mathrm {def} }{{}={}}}{\frac {d\phi }{dt}}(t).

因此，瞬時頻率（单位赫兹）为：

f(t){\stackrel {\mathrm {def} }{{}={}}}{\frac {1}{2\pi }}\omega (t).

[3]

瞬时振幅、瞬时相位与频率在一些应用中用于测量和检测的信号的局部特征。信号的解析表示的另一个应用与调制信号的解调有关。极坐标方便将振幅調變和相位（或频率）调制的影响分开，对解调某些种类的信号很有效。

复包络/基带

解析信号通常都会在频率上移位（下转换）到 0 Hz，可能会产生[非对称]负频率分量：

{\underline {s_{\mathrm {a} }}}(t){\stackrel {\mathrm {def} }{{}={}}}s_{\mathrm {a} }(t)e^{-j\omega _{0}t}=s_{\mathrm {m} }(t)e^{j(\phi (t)-\omega _{0}t)},

其中 $\omega _{0}$ 是任意参考角频率。[2]

这个函数有不同的名称，如复包络和复基带。复包络不是唯一的；它是由 $\omega _{0}$ 的选取决定的。这个概念通常用于处理带通信号。如果 $s(t)$ 是调制信号， $\omega _{0}$ 可能会等于它的载波频率。

在其他情况下， $\omega _{0}$ 选在所需通带的中间。因此简单的实系数低通滤波器就可以去除感兴趣的部分。另一个动机是减少最高频率，从而降低最小的无混叠采样率。频移不加大复信号表示的数学处理难度。因此从这个意义上说，下转换的信号仍然是解析信号。但是恢复实值表示不再是简简单单提取实部的问题了。为了避免混疊可能需要上转换，若信号已被（离散时间）采样，还可能需要插值（升採樣）。

若选取的 $\omega _{0}$ 大于 $s_{\mathrm {a} }(t)$ 的最高频率，则 ${\underline {s_{\mathrm {a} }}}(t)$ 没有正频率。在这种情况下，提取实部并恢复它们，但顺序要相反；低频分量现在变为高频分量，反之亦然。这可用于解调一种叫做下边带的单边带信号。

参考频率的其他选择：

有时 $\omega _{0}$ 的选取是要最小化

\int _{0}^{+\infty }(\omega -\omega _{0})^{2}|S_{\mathrm {a} }(\omega )|^{2}\,d\omega .

另外，[4] $\omega _{0}$ 选取还可以是要最小化线性逼近解缠的瞬时相位 $\phi (t)$ 的均方误差：

\int _{-\infty }^{+\infty }[\omega (t)-\omega _{0}]^{2}|s_{\mathrm {a} }(t)|^{2}\,dt

再或者（对最佳 $\theta$ ）：

\int _{-\infty }^{+\infty }[\phi (t)-(\omega _{0}t+\theta )]^{2}\,dt.

在信号处理领域，维格纳–威利分布定义中需要解析信号，因此该方法在实际应用中具有理想特性。[5]

有时复包络与复振幅同义；[lower-alpha 1][lower-alpha 2] 其他时候它作为一种时间无关的推广形式。[lower-alpha 3] 它们的关系并不像实值的情形那样；变化的包络产生恒定的振幅。

参见

希爾伯特轉換
负频率

应用

单边带调制
正交滤波器
因果滤波器

注释

"the complex envelope (or complex amplitude)"[6]
"the complex envelope (or complex amplitude)", p.586 [7]
"Complex envelope is an extended interpretation of complex amplitude as a function of time." p.85[8]

参考文献

``Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition, by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. Copyright © 2014-04-21 by Julius O. Smith III Center for Computer Research in Music and Acoustics (CCRMA), Stanford University, https://ccrma.stanford.edu/~jos/r320/Analytic_Signals_Hilbert_Transform.html[7/16/2014 1:07:57 PM]
Bracewell, Ron. The Fourier Transform and Its Applications. McGraw-Hill, 1965. p269
B. Boashash, "Estimating and Interpreting the Instantaneous Frequency of a Signal-Part I: Fundamentals", Proceedings of the IEEE, Vol. 80, No. 4, pp. 519-538, April 1992
Justice, J. . IEEE Transactions on Acoustics, Speech, and Signal Processing. 1979-12-01, 27 (6): 670–684. ISSN 0096-3518. doi:10.1109/TASSP.1979.1163321.
B. Boashash, “Notes on the use of the Wigner distribution for time frequency signal analysis”, IEEE Trans. on Acoustics, Speech, and Signal Processing , vol. 26, no. 9, 1987
Hlawatsch, Franz; Auger, François. . John Wiley & Sons. 2013-03-01. ISBN 9781118623831 （英语）.
Driggers, Ronald G. . CRC Press. 2003-01-01. ISBN 9780824742508 （英语）.
Okamoto, Kenʼichi. . IOS Press. 2001-01-01. ISBN 9781586031015 （英语）.

延伸阅读

Leon Cohen, Time-frequency analysis, Prentice Hall, Upper Saddle River, 1995.
Frederick W. King, Hilbert Transforms, vol. II, Cambridge University Press, Cambridge, 2009.
B. Boashash, Time-Frequency Signal Analysis and Processing: A Comprehensive Reference, Elsevier Science, Oxford, 2003.

外部链接

Analytic Signals and Hilbert Transform Filters

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[7] "the complex envelope (or complex amplitude)"[6]

[9] "the complex envelope (or complex amplitude)", p.586 [7]

[11] "Complex envelope is an extended interpretation of complex amplitude as a function of time." p.85[8]

[1] ``Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition, by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. Copyright © 2014-04-21 by Julius O. Smith III Center for Computer Research in Music and Acoustics (CCRMA), Stanford University, https://ccrma.stanford.edu/~jos/r320/Analytic_Signals_Hilbert_Transform.html[7/16/2014 1:07:57 PM]

[Bracewell-2] Bracewell, Ron. The Fourier Transform and Its Applications. McGraw-Hill, 1965. p269

[3] B. Boashash, "Estimating and Interpreting the Instantaneous Frequency of a Signal-Part I: Fundamentals", Proceedings of the IEEE, Vol. 80, No. 4, pp. 519-538, April 1992

[4] Justice, J. . IEEE Transactions on Acoustics, Speech, and Signal Processing. 1979-12-01, 27 (6): 670–684. ISSN 0096-3518. doi:10.1109/TASSP.1979.1163321.

[5] B. Boashash, “Notes on the use of the Wigner distribution for time frequency signal analysis”, IEEE Trans. on Acoustics, Speech, and Signal Processing , vol. 26, no. 9, 1987

[6] Hlawatsch, Franz; Auger, François. . John Wiley & Sons. 2013-03-01. ISBN 9781118623831 （英语）.

[8] Driggers, Ronald G. . CRC Press. 2003-01-01. ISBN 9780824742508 （英语）.

[10] Okamoto, Kenʼichi. . IOS Press. 2001-01-01. ISBN 9781586031015 （英语）.