類球面
類球面是一種二次曲面。二維的橢圓有兩個主軸,稱為長軸與短軸。在三維空間裏,將一個橢圓繞著其任何一主軸旋轉,則可得到一個類球面。
- 假若,這旋轉主軸是長軸,則這個類球面為長球面。例如,英式足球裏所用的橄欖球是長球形狀。
- 假若,這旋轉主軸是短軸,則這個類球面為扁球面。例如,地球在北極與南極稍微有點扁平,在赤道又有點凸漲。所以,地球是扁球形狀。
- 假若,生成的橢圓是圓圈,則這個類球面為完全對稱的圓球面。
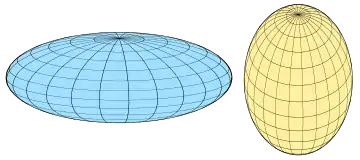 | ||
| 扁球面 | 長球面 | |
|---|---|---|
方程式
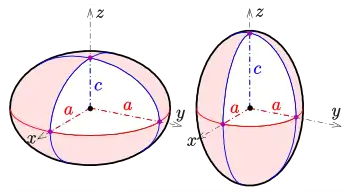
对类球面半轴的赋值。如果c < a则为扁球面(左图)而如果c > a则为长球面(右图)。
用另外一種方法來描述,類球面是一種橢球面。採用直角坐標,橢球面可以表達為
- ;
其中,與分別是橢球面在x-軸與y-軸的赤道半徑,是橢球面在z-軸的極半徑,這三個正值實數的半徑決定了橢球面的形狀。 以z-轴为旋转轴的类球面,它的方程为:
- 。
- 假若,三個半徑都相等,則這橢球面是圓球面:
- 。
- 假若,類球面的赤道半徑小於極半徑,則這是類球面是長球面:
- 。
- 假若,類球面的赤道半徑大於極半徑,則這是類球面是扁球面:
- 。
性质
體積
類球的體積是。
引用
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
