黑体辐射
黑体辐射指处于热力学平衡态的黑体发出的电磁辐射。黑体辐射的电磁波谱只取决于黑体的温度。另一方面,所謂黑體輻射是光和物質達到平衡所表現出的現象。物質達到平衡,所以可以用一個溫度來描述物質的狀態,而光和物質的交互作用很強,如此光和光之間也可以用一個溫度來描述(光和光之間本身不會有交互作用,但光和物質的交互作用很強),而描述這關係的便是普朗克分佈(Planck distribution)。黑体辐射能量按波长的分布仅与温度有关。
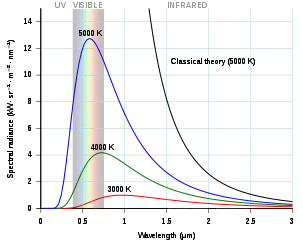
黑体不仅仅能全部吸收外来的电磁辐射,且散射电磁辐射的能力比同温度下的任何其它物体强。对于黑体的研究,使自然现象中的量子效应被發现。而黑体作为一个理想化的物体,在现实中是不存在的,因此现实中物体的辐射也与理论上的黑体辐射有所出入。但是,可以观察一些非常类似黑体的物质发出的辐射,例如一顆恆星或一個只有單一開口的空腔所发出的辐射。舉個例來說,人們觀測到宇宙背景輻射,對應到一個約3K的黑體輻射,這暗示宇宙早期光是和物質達到平衡的。而隨著時間演化,溫度慢慢降了下來,但方程式依然存在。(頻率和溫度的效應抵銷)
黑體輻射方程
黑体辐射本领
古斯塔夫·基爾霍夫证明,对于任意一个物体,辐射本领与吸收率之比是一个与组成物体的物质无关的普适函数(以表示)
其中,辐射本领为单位时间内从辐射体表面的单位面积上发射出的辐射能量的频率分布,所以,在的时间,从面积上发射出频率在范围内的能量为。因此的单位为,可以证明,黑体辐射本领与辐射体的能量密度分布的关系为
的单位为 吸收率则为照到物体上的辐射能量分布被吸收的份额,由於黑体的吸收率为1,所以它的辐射本领
这意味着黑体辐射本领等价于普适函数(与物质无关) 同时也可以以用来表达辐射本领
黑體輻射的維恩位移定律
維恩位移定律表述了不同溫度的黑體波譜之間的聯繫。一旦某一個溫度下的黑體波譜形狀已知,則可通過維恩位移定律推導出同一黑體在其它溫度下的波譜形狀。
維恩位移定律計算出黑體輻射強度達到最大時的波長,,這個物理量只和黑體的溫度相關:
其中b为比例常数,称为维恩位移常数,数值等于2.897 7721(26)×10–3 m K(2010年国际科技数据委员会推荐值,括号中为68.27%置信度下的不确定尾数)。
注意到強度的峰值可以表達為單位波長強度或是單位頻率強度,在維恩位移定律中使用的是單位波長強度的表達式,而在上面的普朗克黑體輻射定律中則使用的是單位頻率強度。單位頻率能量達到最大時的波長為
黑體輻射的斯特藩-玻爾茲曼定律
這條定理指出,一個黑體表面單位面積放出的能量正比於其絕對溫度的4次方:
其中
:單位面積单位时间所放出的總能量,[ ]
:黑體的絕對溫度,[K ]
:斯特藩-玻爾茲曼常數,
人體的輻射
 |
 |
| 人體的大多數能量以紅外線的形式散射掉了。一些材料對可見光是不透明的,但是對紅外線卻沒有任何遮蓋能力(注意照片中的垃圾袋),相反另一些材料對可見光是透明的,反而會對紅外線產生阻擋或反射(注意照片中人物的眼鏡)。 |
黑體輻射同樣適用於人體,因為人體的一部分能量以電磁波的形式散射出體表,其中大部分為紅外線。
净放射功率是吸收功率和放出功率的差值:
代入黑體輻射的斯特藩-玻爾茲曼定律:
人體的表面積約為2平方米,皮膚和大多數衣物(非金屬材質)中,遠紅外線熱發射率基本相同。[7][8]皮膚的溫度大概為33℃,[9]但在約為20℃的環境溫度影響下,衣物會使體表溫度降為大約28℃。[10]因此,人體的净放射功率约為
人體一天以上述放射方式放出的總能量大約為 9000 千焦(100 W 乘以 86400 秒),即2000千卡。一個40歲的成年人的基礎代謝率約為35千卡/(米2·小時),[11]即為1700千卡每天(以2平方米為基準)。實際上即便是靜坐的成年人每日的平均代謝率也比基礎代謝率高出约50%到70%。[12]
熱對流和體液蒸發也是人體散失能量的重要因素。因為努塞爾特數遠遠大於單位一,所以熱傳導可以忽略。蒸發(汗液)這個要素只有在熱輻射和熱對流在某個恆溫環境內不起主導因素時才給予考慮。自由熱傳導率儘管比輻射率小,但是也是可以進行比較的。[13]因此,人體在靜止涼爽的環境中散失的總熱能的三分之二是由於熱輻射導致的。由於使用了很多假設情況下的近似值,所以這個結果只能算是粗略的估計。人體周圍的空氣運動所引起的對流或是體液蒸發同樣和熱輻射一樣是導致體能流失的重要因素。
如果在人體這個黑體上使用維恩位移定律,可以得到人體放出輻射的波長峰值為:
- .
這個結果可以解釋為什麼人體熱像儀的波長一般設為非常靈敏的7000到14000納米。
行星和其衛星之間的熱力學關係
黑體輻射定理的應用之一是用於概略的估計一個行星的溫度。其表面可能由於溫室效應而比估計溫度高。[14]
因素

行星的溫度主要和以下幾個因素相關:
所有的輻射,無論是行星內部產生的,其他恆星還是其本身放出的,對行星的溫度都有很重要的影響。以下的推導即著重討論輻射。
推導
首先使用斯特藩-玻爾茲曼定律得到太陽放射出的總功率(能量/秒):
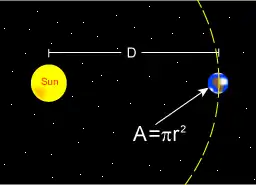
其中
- :斯特藩-玻尔兹曼常数
- : 太陽的表面溫度
- : 太陽的半徑
太陽平均的向各個方向放出能量,因此,地球實際上只是接受到其中很小的一部分。這部分能量為(指接觸到大氣層外部):
其中
- :地球的半徑
- :天文單位, 太陽與地球的平均距離
由於本身的高溫,太陽發出的射線大多數屬於紫外線和可見光(UV-Vis)頻率範圍。在這個頻率範圍內,地球會反射一部分能量,其數量為,即地球對UV-Vis範圍射線的反照率。反過來,即地球吸收了的太陽光,並反射了剩下的。地球和其大氣層所吸收的能量為:
雖然地球僅僅以一個面積為的圓形區域進行吸收,但是它同時以一個球體的形態向各個方向放出能量。假設地球是一個完全黑體,它將遵循斯特藩-玻爾茲定理:
其中是地球的溫度。由於地球的溫度明顯低於太陽,其放射的多為光系的紅外線(IR)部分。在這個頻率範圍內,地球會放出黑體總放射波的一部分,大約為,是紅外線頻率的平均放射率。因此地球和其大氣層實際放出的能量為:
假設地球處於熱平衡,則吸收的能量等於放射的能量:
代入所有關於太陽和地球能量的表達式(1-5)可以得到:
換句話說,考慮到所有的估計值,地球的溫度與下列因素有關:太陽的表面溫度,太陽的半徑,日地間距,以及地球的反照率和紅外發射率。
地球的溫度
如果代入對太陽和地球的測量值:
並將平均放射率設為單位量,可以得到地球的“有效溫度”為:
- 254.356 K or -18.8 ℃.
這個溫度值是基於地球是一個完全黑體的假設,忽略溫室效應並認為地球的反照率完全不變的基礎上得到的。而實際上地球僅是非常接近一個完美黑體,所以必須將估計溫度定為比有效溫度高出好幾度。如果想要估計地球在沒有大氣層的情況下的溫度,可以使用月球的反照率和發射率進行計算。月球的反照率和發射率大約為0.1054[16]和0.95[17], 因此,可以得到這種情況下的溫度約為1.36 ℃. 地球的平均反照率的估計值在0.3–0.4之間,由此可以得到不同的估計溫度。進行計算時相較於太陽的溫度,尺寸和日地距離,人們更加常用日照常量(總日照量密度)。比如使用0.4為反照率並使用日照量密度1400 W m−2,可以得到約為245K的地球溫度。[18]同理,如果使用0.3的反照率以及1372 W m−2的日照常量,地球溫度為255 K。[19][20]
運動黑體的多普勒效應
多普勒效應是著名的物理現象,人們用它來描述當一個光源對觀察者作相對運動時,其光線頻率的變化。若一單色光源的發射頻率為f,則當它相對觀察者做相對運動時,觀察者看起來其頻率為f':
其中v是這個光源對觀察者的相對速度,θ是速度向量和觀察者及光源間連線的夾角,c為光速。[21]上面的公式為總公式,還可以從其得到一些更簡單的特殊例子,如光源直接向觀察者移動(θ = π) 或是離開觀察者(θ = 0),當然其移動速度遠遠小於c。
參考文獻
- 曾谨言. 量子力学教程. 北京:科学出版社,2003
- 张启仁. 量子力学. 北京:科学出版社.2002
- 张汝铿. 量子力学.上海:复旦大学出版社.1997
- 关洪. 量子力学基础. 北京:高等教育出版社.1999
- 程□生. 现代量子力学教程 北京大学出版社.2006
- (Rybicki & Lightman 1979,p.22)
- Infrared Services. . [2007-06-24]. (原始内容存档于2007-06-25).
- Omega Engineering. . [2007-06-24]. (原始内容存档于2007-06-28).
- Farzana, Abanty. . The Physics Factbook. 2001 [2007-06-24]. (原始内容存档于2007-06-29).
- Lee, B. (PDF). [2007-06-24]. (原始内容 (PDF)存档于2007-06-27).
- Harris J, Benedict F. . Proc Natl Acad Sci USA. 1918, 4 (12): 370–3. PMC 1091498. PMID 16576330. doi:10.1073/pnas.4.12.370.
- Levine, J. . Am J Physiol Endocrinol Metab. 2004, 286 (5): E675–E685 [2013-05-26]. PMID 15102614. doi:10.1152/ajpendo.00562.2003. (原始内容存档于2010-06-27).
- DrPhysics.com. . [2007-06-24]. (原始内容存档于2007-06-23).
- Cole, George H. A.; Woolfson, Michael M. . Institute of Physics Publishing. 2002: 36–37, 380–382 [2013-05-26]. ISBN 0-7503-0815-X. (原始内容存档于2014-09-28).
- . [2013-05-26]. (原始内容存档于2010-07-15).
- Saari, JM; Shorthill, RW. .5..161S/0000167.000.html 请检查
|url=值 (帮助). The Moon. 1972, 5 (1-2): 161–178. doi:10.1007/BF00562111. - Lunar and Planetary Science XXXVII (2006) 2406
- Michael D. Papagiannis. . Taylor & Francis. 1972: 10–11 [2013-05-26]. ISBN 9780677040004. (原始内容存档于2014-09-26).
- Willem Jozef Meine Martens and Jan Rotmans. . Springer. 1999: 52–55 [2013-05-26]. ISBN 9780792359968. (原始内容存档于2014-10-01).
- F. Selsis. . Pascale Ehrenfreund; 等 (编). . Springer. 2004: 279–280 [2013-05-26]. ISBN 9781402025877. (原始内容存档于2014-09-30).
- The Doppler Effect, TP Gill, Logos Press, 1965