QR分解

Householder变换将一个向量关于某个平面或者超平面进行反射。我们可以利用这个操作对${\displaystyle m\times n(m\geqq n)}$的矩阵${\displaystyle A}$进行QR分解。

矩阵${\displaystyle Q}$可以被用于对一个向量以一种特定的方式进行反射变换，使得它除了一个维度以外的其他所有分量都化为0。

令${\displaystyle \mathbf {x} }$为矩阵${\displaystyle A}$的任一m维实列向量，且有${\displaystyle \|\mathbf {x} \|=|\alpha |}$（其中${\displaystyle \alpha }$为标量）。若该算法是通过浮点数实现的，则${\displaystyle \alpha }$应当取和${\displaystyle \mathbf {x} }$的第${\displaystyle k}$维相反的符号（其中${\displaystyle x_{k}}$是要保留不为0的项），这样做可以避免精度缺失。对于复数的情况，令

${\displaystyle \alpha =-\mathrm {e} ^{\mathrm {i} \arg x_{k}}\|\mathbf {x} \|}$

（Stoer & Bulirsch 2002，p.225），并且在接下来矩阵${\displaystyle Q}$的构造中要将矩阵转置替换为共轭转置。

接下来，设${\displaystyle \mathbf {e} _{1}}$为单位向量${\displaystyle (1,0,\cdots ,0)^{T}}$，||·||为欧几里德范数，${\displaystyle I}$为${\displaystyle m\times m}$单位矩阵，令

${\displaystyle \mathbf {u} =\mathbf {x} -\alpha \mathbf {e} _{1}}$ ，

${\displaystyle \mathbf {v} ={\mathbf {u} \over \|\mathbf {u} \|}}$ ，

${\displaystyle Q=I-2\mathbf {v} \mathbf {v} ^{T}}$ 。

或者，若${\displaystyle A}$为复矩阵，则

${\displaystyle Q=I-(1+w)\mathbf {v} \mathbf {v} ^{H}}$，其中${\displaystyle w=\mathbf {x} ^{H}\mathbf {v} \mathbf {/} \mathbf {v} ^{H}\mathbf {x} }$

式中${\displaystyle \mathbf {x} ^{H}}$是${\displaystyle x}$的共轭转置（亦称埃尔米特共轭或埃尔米特转置）。

则${\displaystyle Q}$为一个${\displaystyle m\times m}$的Householder矩阵，它满足

${\displaystyle Q\mathbf {x} =(\alpha ,0,\cdots ,0)^{T}\ }$

利用Householder矩阵，可以将一个${\displaystyle m\times n}$的矩阵${\displaystyle A'}$变换为上三角矩阵。 首先，我们将A左乘通过选取矩阵的第一行得到行向量${\displaystyle x}$的Householder矩阵${\displaystyle Q_{1}}$。这样，我们得到的矩阵${\displaystyle Q_{1}A}$的第一列将全部为0（第一行除外）：

${\displaystyle Q_{1}A={\begin{bmatrix}\alpha _{1}&\star &\dots &\star \\0&&&\\\vdots &&A'&\\0&&&\end{bmatrix}}}$

这个过程对于矩阵${\displaystyle A'}$（即${\displaystyle Q_{1}A}$排除第一行和第一列之后剩下的方阵）还可以继续做下去，从而得到另一个Householder矩阵${\displaystyle Q_{2}}$。注意到${\displaystyle Q_{2}}$其实比${\displaystyle Q_{1}}$要小，因为它是在${\displaystyle Q_{1}A}$而非${\displaystyle A}$的基础上得到的。因此，我们需要在${\displaystyle Q_{2}}$的左上角补上1，或者，更一般地来说：

${\displaystyle Q_{k}={\begin{bmatrix}I_{k-1}&0\\0&Q_{k}'\end{bmatrix}}}$

将这个迭代过程进行${\displaystyle t}$次之后（${\displaystyle t=\min(m-1,n)}$）,将有

${\displaystyle R=Q_{t}\cdots Q_{2}Q_{1}A}$

其中R为一个上三角矩阵。因此，令

${\displaystyle Q=Q_{1}^{T}Q_{2}^{T}\cdots Q_{t}^{T},}$

则${\displaystyle A=QR}$为矩阵${\displaystyle A}$的一个QR分解。

相比与Gram-Schmidt正交化，使用Householder变换具有更好的数值稳定性。

现在要用Householder变换求解矩阵${\displaystyle A}$的${\displaystyle QR}$ 分解。

${\displaystyle A={\begin{bmatrix}0&3&1\\0&4&-2\\2&1&1\\\end{bmatrix}}}$

因为${\displaystyle \alpha _{1}=[0,\ 0,\ 2]^{T}}$, 令${\displaystyle a_{1}=||\alpha _{1}||_{2}=2}$，则

${\displaystyle \omega _{1}={\frac {\alpha _{1}-a_{1}e_{1}}{||\alpha _{1}-a_{1}e_{1}||_{2}}}={\frac {1}{\sqrt {2}}}[-1,\ 0,\ 1]^{T}}$

则有

${\displaystyle H_{1}=I-2\omega _{1}\omega _{1}^{H}{\begin{bmatrix}0&0&1\\0&1&0\\1&0&0\\\end{bmatrix}}}$

从而，

${\displaystyle H_{1}A={\begin{bmatrix}2&1&2\\0&4&-2\\0&3&1\\\end{bmatrix}}}$

记${\displaystyle \beta =[4,\ 3]^{T}}$, 则${\displaystyle b_{2}=||\beta _{2}||_{2}=5}$。令

${\displaystyle \omega _{2}={\frac {\beta _{2}-b_{1}e_{2}}{||\beta _{2}-b_{1}e_{2}||_{2}}}={\frac {1}{\sqrt {10}}}[-1,\ 3]^{T}}$

${\displaystyle {\hat {H_{2}}}=I-2\omega _{2}\omega ^{H}={\frac {1}{5}}{\begin{bmatrix}4&3\\3&-4\\\end{bmatrix}}}$

记，

${\displaystyle H_{2}={\begin{bmatrix}1&0^{T}\\0&{\hat {H_{2}}}\\\end{bmatrix}}={\begin{bmatrix}1&0&0\\0&4&3\\0&3&-4\\\end{bmatrix}}}$

则，

${\displaystyle R=H_{2}(H_{1}A)={\begin{bmatrix}2&1&2\\0&5&-1\\0&0&-2\\\end{bmatrix}}}$

那么

${\displaystyle Q=H_{1}H_{2}={\frac {1}{5}}{\begin{bmatrix}0&3&-4\\0&4&3\\5&0&0\\\end{bmatrix}}}$

吉文斯旋转表示为如下形式的矩阵

${\displaystyle G(i,j,\theta )={\begin{bmatrix}1&\cdots &0&\cdots &0&\cdots &0\\\vdots &\ddots &\vdots &&\vdots &&\vdots \\0&\cdots &c&\cdots &s&\cdots &0\\\vdots &&\vdots &\ddots &\vdots &&\vdots \\0&\cdots &-s&\cdots &c&\cdots &0\\\vdots &&\vdots &&\vdots &\ddots &\vdots \\0&\cdots &0&\cdots &0&\cdots &1\end{bmatrix}}}$

这里的 c = cos(θ) 和 s = sin(θ) 出现在第 i 行和第 j 行与第 i 列和第 j 列的交叉点上。就是说，吉文斯旋转矩阵的所有非零元定义如下：:

${\displaystyle {\begin{aligned}g_{k\,k}&{}=1\qquad {\text{for}}\ k\neq i,\,j\\g_{i\,i}&{}=c\\g_{j\,j}&{}=c\\g_{i\,j}&{}=s\\g_{j\,i}&{}=-s\end{aligned}}}$

乘积 G(i, j, θ)x 表示向量 x 在 (i,j)平面中的逆时针旋转 θ 弧度。

对于一个向量

${\displaystyle {\begin{array}{lcl}A&=&{\begin{bmatrix}a\\b\\\end{bmatrix}}\\\end{array}}}$

如果，${\displaystyle r={\sqrt {a^{2}+b^{2}}}}$ , ${\displaystyle c={\frac {a}{r}}}$ , ${\displaystyle s=-{\frac {b}{r}}}$ , 那么，就存在旋转矩阵G，使${\displaystyle A}$ 底部转成0。

${\displaystyle A_{2\_Sub}={\begin{bmatrix}c&-s\\s&c\\\end{bmatrix}}{\begin{bmatrix}a\\b\\\end{bmatrix}}={\begin{bmatrix}r\\0\\\end{bmatrix}}}$

每一次的旋转，吉文斯旋转都可以将一个元素化成0，直到将原始矩阵转成一个上三角矩阵，则完成分解。

${\displaystyle A=QR}$

${\displaystyle Q=G_{1}^{T}G_{2}^{T}\cdots G_{k}^{T}}$

${\displaystyle A_{1}={\begin{bmatrix}6&5&0\\5&1&4\\0&4&3\\\end{bmatrix}}}$

${\displaystyle r={\sqrt {6^{2}+5^{2}}}\approx 7.8102}$

${\displaystyle c=6/r\approx 0.7682}$

${\displaystyle s=-5/r\approx -0.6402}$

${\displaystyle A_{2}=G_{1}A_{1}={\begin{bmatrix}c&-s&0\\s&c&0\\0&0&1\\\end{bmatrix}}{\begin{bmatrix}6&5&0\\5&1&4\\0&4&3\\\end{bmatrix}}\approx {\begin{bmatrix}7.8102&4.4813&2.5607\\0&-2.4327&3.0729\\0&4&3\\\end{bmatrix}}}$

对于:${\displaystyle A_{2}}$子矩阵 :${\displaystyle A_{2\_Sub}}$

${\displaystyle A_{2\_Sub}={\begin{bmatrix}-2.4327&3.0729\\4&3\\\end{bmatrix}}}$

${\displaystyle r={\sqrt {(-2.4327)^{2}+4^{2}}}\approx 4.6817}$

${\displaystyle c=-2.4327/r\approx -0.5196}$

${\displaystyle s=-5/r\approx -0.8544}$

${\displaystyle G_{2}A_{2}={\begin{bmatrix}1&0&0\\0&c&-s\\0&s&c\\\end{bmatrix}}{\begin{bmatrix}7.8102&4.4813&2.5607\\0&-2.4327&3.0729\\0&4&3\\\end{bmatrix}}\approx {\begin{bmatrix}7.8102&4.4813&2.5607\\0&4.6817&0.9664\\0&0&-4.1843\\\end{bmatrix}}}$

${\displaystyle R=G_{2}A_{2}=G_{2}G_{1}A_{1}}$

${\displaystyle Q=G_{1}^{T}G_{2}^{T}={\begin{bmatrix}0.7682&0.3327&0.5470\\0.6402&-0.3992&-0.6564\\0&0.8544&-0.5196\\\end{bmatrix}}}$

图1 ${\displaystyle {\boldsymbol {v}}}$在${\displaystyle {\boldsymbol {V}}^{2}}$上投影，构造${\displaystyle {\boldsymbol {V}}^{3}}$上的正交基${\displaystyle {\boldsymbol {\beta }}}$

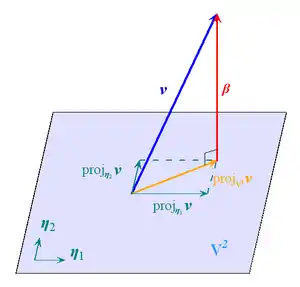
格拉姆-施密特正交化的基本想法，是利用投影原理在已有正交基的基础上构造一个新的正交基。

设${\displaystyle {\boldsymbol {v}}\in {\boldsymbol {V^{n}}}}$。${\displaystyle {\boldsymbol {V}}^{k}}$是${\displaystyle {\boldsymbol {V}}^{n}}$上的${\displaystyle k}$维子空间，其标准正交基为${\displaystyle \{{\boldsymbol {\eta }}_{1},\ldots ,{\boldsymbol {\eta }}_{k}\}}$，且${\displaystyle {\boldsymbol {v}}}$不在${\displaystyle {\boldsymbol {V}}^{k}}$上。由投影原理知，${\displaystyle {\boldsymbol {v}}}$与其在${\displaystyle {\boldsymbol {V}}^{k}}$上的投影${\displaystyle \mathrm {proj} _{\boldsymbol {V^{k}}}{\boldsymbol {v}}}$之差

${\displaystyle {\boldsymbol {\beta }}={\boldsymbol {v}}-\sum _{i=1}^{k}\mathrm {proj} _{{\boldsymbol {\eta }}_{i}}\,{\boldsymbol {v}}={\boldsymbol {v}}-\sum _{i=1}^{k}\langle {\boldsymbol {v}},{\boldsymbol {\eta }}_{i}\rangle {\boldsymbol {\eta }}_{i}}$

是正交于子空间${\displaystyle {\boldsymbol {V}}^{k}}$的，亦即${\displaystyle {\boldsymbol {\beta }}}$正交于${\displaystyle {\boldsymbol {V}}^{k}}$的正交基${\displaystyle {\boldsymbol {\eta }}_{i}}$。因此只要将${\displaystyle {\boldsymbol {\beta }}}$单位化，即

${\displaystyle {\boldsymbol {\eta }}_{k+1}={\frac {\boldsymbol {\beta }}{\|{\boldsymbol {\beta }}\|}}={\frac {\boldsymbol {\beta }}{\sqrt {\langle {\boldsymbol {\beta }},{\boldsymbol {\beta }}\rangle }}}}$

那么${\displaystyle \{{\boldsymbol {\eta }}_{1},\ldots ,{\boldsymbol {\eta }}_{k},{\boldsymbol {\eta }}_{k+1}\}}$就是${\displaystyle {\boldsymbol {V}}^{k}}$在${\displaystyle {\boldsymbol {v}}}$上扩展的子空间${\displaystyle \mathrm {span} \{{\boldsymbol {v}},{\boldsymbol {\eta }}_{1},...,{\boldsymbol {\eta }}_{k}\}}$的标准正交基。

根据上述分析，对于向量组${\displaystyle \{{\boldsymbol {v}}_{1},\ldots ,{\boldsymbol {v}}_{m}\}}$张成的空间${\displaystyle {\boldsymbol {V}}^{m}}$ (${\displaystyle m<n}$)，只要从其中一个向量（不妨设为${\displaystyle {\boldsymbol {v}}_{1}}$）所张成的一维子空间${\displaystyle \mathrm {span} \{{\boldsymbol {v}}_{1}\}}$开始（注意到${\displaystyle {\boldsymbol {v}}_{1}}$就是${\displaystyle \mathrm {span} \{{\boldsymbol {v}}_{1}\}}$的正交基），重复上述扩展构造正交基的过程，就能够得到${\displaystyle {\boldsymbol {V}}^{n}}$ 的一组正交基。这就是格拉姆-施密特正交化。

首先需要确定已有基底向量的顺序，不妨设为${\displaystyle \{{\boldsymbol {v}}_{1},\ldots ,{\boldsymbol {v}}_{n}\}}$。Gram-Schmidt正交化的过程如下：

	${\displaystyle {\boldsymbol {\beta }}_{1}={\boldsymbol {v}}_{1},}$		${\displaystyle {\boldsymbol {\eta }}_{1}={{\boldsymbol {\beta }}_{1} \over \|{\boldsymbol {\beta }}_{1}\|}}$
	${\displaystyle {\boldsymbol {\beta }}_{2}={\boldsymbol {v}}_{2}-\langle {\boldsymbol {v}}_{2},{\boldsymbol {\eta }}_{1}\rangle {\boldsymbol {\eta }}_{1},}$		${\displaystyle {\boldsymbol {\eta }}_{2}={{\boldsymbol {\beta }}_{2} \over \|{\boldsymbol {\beta }}_{2}\|}}$
	${\displaystyle {\boldsymbol {\beta }}_{3}={\boldsymbol {v}}_{3}-\langle {\boldsymbol {v}}_{3},{\boldsymbol {\eta }}_{1}\rangle {\boldsymbol {\eta }}_{1}-\langle {\boldsymbol {v}}_{3},{\boldsymbol {\eta }}_{2}\rangle {\boldsymbol {\eta }}_{2},}$		${\displaystyle {\boldsymbol {\eta }}_{3}={{\boldsymbol {\beta }}_{3} \over \|{\boldsymbol {\beta }}_{3}\|}}$
	${\displaystyle \vdots }$		${\displaystyle \vdots }$
	${\displaystyle {\boldsymbol {\beta }}_{n}={\boldsymbol {v}}_{n}-\sum _{i=1}^{n-1}\langle {\boldsymbol {v}}_{n},{\boldsymbol {\eta }}_{i}\rangle {\boldsymbol {\eta }}_{i},}$		${\displaystyle {\boldsymbol {\eta }}_{n}={{\boldsymbol {\beta }}_{n} \over \|{\boldsymbol {\beta }}_{n}\|}}$

这样就得到${\displaystyle \mathrm {span} \{{\boldsymbol {v}}_{1},\ldots ,{\boldsymbol {v}}_{n}\}}$上的一组正交基${\displaystyle \{{\boldsymbol {\beta }}_{1},\ldots ,{\boldsymbol {\beta }}_{n}\}}$，以及相应的标准正交基${\displaystyle \{{\boldsymbol {\eta }}_{1},\ldots ,{\boldsymbol {\eta }}_{n}\}}$。

现在要用格拉姆-施密特变换求解矩阵${\displaystyle A}$的${\displaystyle QR}$ 分解。

${\displaystyle A={\begin{bmatrix}1&2&4\\0&0&5\\0&3&6\\\end{bmatrix}}}$

令， ${\displaystyle a=[1,0,0]}$

${\displaystyle q_{1}={\frac {a}{||a||}}={\begin{bmatrix}1\\0\\0\\\end{bmatrix}}}$

${\displaystyle {\hat {q_{2}}}=b-(b*q_{1})q_{1}={\begin{bmatrix}2\\0\\3\\\end{bmatrix}}-2{\begin{bmatrix}1\\0\\0\\\end{bmatrix}}={\begin{bmatrix}0\\0\\3\\\end{bmatrix}}}$

${\displaystyle q_{2}={\frac {\hat {q_{2}}}{||{\hat {q_{2}}}||}}={\begin{bmatrix}0\\0\\1\\\end{bmatrix}}}$

${\displaystyle {\hat {q_{3}}}=c-(c*q_{1})q_{1}-(c*q_{2})q_{2}={\begin{bmatrix}4\\5\\6\\\end{bmatrix}}-4{\begin{bmatrix}1\\0\\0\\\end{bmatrix}}-6{\begin{bmatrix}0\\0\\1\\\end{bmatrix}}={\begin{bmatrix}0\\5\\0\\\end{bmatrix}}}$

${\displaystyle q_{3}={\frac {\hat {q_{3}}}{||{\hat {q_{3}}}||}}={\begin{bmatrix}0\\1\\0\\\end{bmatrix}}}$

那么可知，

${\displaystyle Q={\begin{bmatrix}1&0&0\\0&0&1\\0&1&0\\\end{bmatrix}}}$

由${\displaystyle A=QR}$，可知，

${\displaystyle R={\begin{bmatrix}1&2&4\\0&3&6\\0&0&5\\\end{bmatrix}}}$

对于直接求解线性方程组的逆，用QR分解的方法求解会更具有数据的稳定性。 对于求解一个线性系统${\displaystyle Ax=b}$, 这里${\displaystyle A}$的维度是${\displaystyle m\times n}$。

如果${\displaystyle m\leq n}$, 那么${\displaystyle A^{T}=QR}$,这里${\displaystyle Q^{T}=Q^{-1}}$)。

${\displaystyle R}$ 的形式是 ${\displaystyle R={\begin{bmatrix}R_{1}\\0\end{bmatrix}}}$，${\displaystyle R_{1}}$是${\displaystyle R}$上不为0的部分。 那么对于

${\displaystyle x=Q{\begin{bmatrix}\left(R_{1}^{\textsf {T}}\right)^{-1}b\\0\end{bmatrix}}}$

如果${\displaystyle m>n}$, 那么${\displaystyle A=QR}$,这里${\displaystyle Q^{T}=Q^{-1}}$)。本质是最小化${\displaystyle ||A{\hat {x}}-b||}$

${\displaystyle {\hat {x}}=R_{1}^{-1}\left(Q_{1}^{\textsf {T}}b\right)}$