一角形
一角形是多邊形的一種。只有1條邊,1個頂點的圖形。在施萊夫利符號中利用{1}來表示。由於一角形沒有内角並且只有一條邊,因此所有一角形都是正一角形。
| 一角形 | |
|---|---|
 圓上,一個一角形是具有單個頂點,和一個360度的圓弧曲面細分。 | |
| 類型 | 正多邊形 |
| 邊 | 1 |
| 頂點 | 1 |
| 施萊夫利符號 | {1} |
| 考克斯特圖 | |
| 對偶 | 自身 |
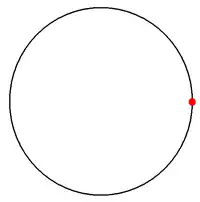
圓形上的正一角形

平面上的正一角形只有一個點
球面幾何學
在球面幾何學中,一角形可以在球面上繪出。 當兩個一角形在球面上形成多邊形二面體,擁有同一個邊和頂點;在施萊夫利符號中利用{1,2}來表示。
| 密鋪 | 本身 | |
|---|---|---|
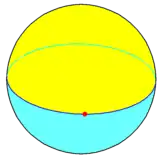 {1,2} |
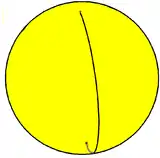 {2,1} |
 {1,1} |
| (F:2, E:1, V=1) | (F:1, E:1, V=2) | (F:1, E:0, V=1) |
參考來源
- Herbert Busemann, The geometry of geodesics. New York, Academic Press, 1955
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
