七面體
在幾何學中,七面體是指由7個面組成的多面體。沒有任何一種七面體是正七面體,也就是說找不到所有面全等、所有邊等長、所有角相等的七面體,有一種等邊的單正的七面體,由四個三角形和三個四邊形組成,其與羅馬曲面拓樸同構[1][2] 。此外亦存有等邊等角的七面體,即五角柱,有時會稱為半正七面體,但不會將它看作是阿基米德立體[3]。
| 部分的七面體 | |
|---|---|
 正五角柱 |
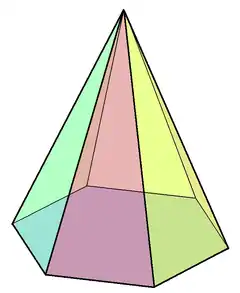 六角錐 |
 五角柱 |
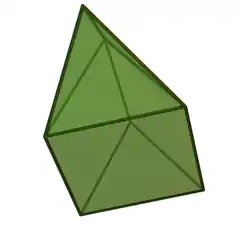 正三角錐柱 |
常見的七面體
常見的七面體有六角錐、五角柱、正三角錐柱、希洛西七面體以及一些剪邊的八面體[4]等多面體。
五角柱
五角柱是一種底面為五邊形的柱體,由7個面15條邊和10個頂點組成。正五角柱代表每個面都是正多邊形的五角柱,其每個頂點都是2個正方形和1個五邊形的公共頂點,因此具有每個角等角的性質,可以歸類為半正七面體。
六角錐
六角錐是一種底面為六邊形的錐體,其具有7個面、14條邊和7個頂點,其對偶多面體是自己本身。正六角錐是一種底面為正六邊形的六角錐。
其他七面體
| 名稱 | 種類 | 圖像 | 符號 | 頂點 | 邊 | 面 | χ | 面的種類 | 對稱性 | 展開圖 |
|---|---|---|---|---|---|---|---|---|---|---|
| 六角錐 | 錐體 |  |
( ) ∨ {6} | 7 | 12 | 7 | 2 | 1個六邊形 6個三角形 |
C6v, [6], (*66) | |
| 五角柱 | 柱體 |  |
t{2,5} {5}x{} |
10 | 15 | 7 | 2 | 2個五邊形 5個矩形 |
D5h, [5,2], (*522), order 20 |  |
| 三角錐柱 | 角錐柱 詹森多面體 |
 |
P3+Y3 | 7 | 12 | 7 | 2 | 4個三角形 3個正方形 |
C3v, [3], (*33) |  |
| 三角錐台錐 | 截角雙錐 |  |
7 | 12 | 7 | 2 | 4個三角形 3個梯形 |
C3v, [3], (*33) |  | |
| 四面半六面體 | 星形多面體 | 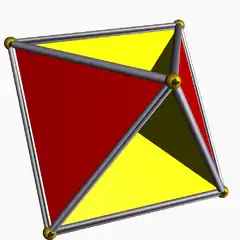 |
2 | 6 | 12 | 7 | 1 | 4個三角形 3個折四邊形 |
Td, [4,3], *432 Td, [3,3], *332 | |
| 西洛希七面體 | 環形多面體 |  |
14[5] | 21[5] | 7[5] | 1 | 3對凹六邊形 1個平行六邊形 |
C1, [ ]+, (11) |  |
非凸七面體
拓樸學中的七面體
共有34種拓樸結構明顯差異的凸七面體[6]。
|
|
|
|
|
|
|
|
六角錐
|
|
|
|
五角柱
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
三角錐柱
|
|
|
|
|
|
|
參考文獻
- Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. New York: Viking Penguin, p. 98, 1991. ISBN 978-0140118131
- Dharwadker, A. "Heptahedron and Roman Surface." 页面存档备份,存于 Electronic Geometry Model No. 2003.05.001.
- 埃里克·韦斯坦因. . MathWorld.
- Holden, A. Shapes, Space, and Symmetry. New York: Dover, p. 95, 1991. ISBN 978-0486268514
- Ace, Tom, , [2016-08-14], (原始内容存档于2016-09-07)
- Counting polyhedra 页面存档备份,存于 numericana.com [2016-1-10]
外部連結
- Polyhedra with 4-7 Faces by Steven Dutch
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
