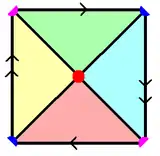
八面體半形

八面體半形可被視為是一種影射多面體，可視為由四個三角形構成的實射影平面鑲嵌，要將其視覺化，可以透過將射影平面構築為一個半球體，其邊界上的對蹠點連結了半球體，並將半球體分成了四等分。 八面體半形也可看成是一個沒有底面的正四角錐。

八面體半形
類別	抽象多胞形 射影多面體
面	4
邊	6
頂點	3
歐拉特徵數	F=4, E=6, V=3 (χ=1)
面的佈局	3.3.3.3
施萊夫利符號	{3,4}/2 or {3,4}3
對稱群	S4, 24階
對偶	立方體半形
特性	不可定向、 歐拉示性數
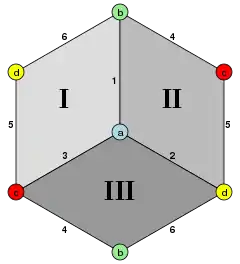立方體半形 (對偶多面體)

在抽象幾何學中，八面體半形是一種抽象正多面體，有著正八面體一半的面。

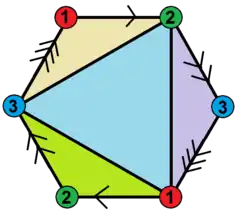
八面體半形有著四個三角形面，六條邊，以及三個頂點。它的對偶多面體為立方體半形

八面體半形可以對稱地表示一個六邊形或一個正方形的施萊格爾圖：

它有著一些特殊的特性：每對頂點之間連接著兩條不同的邊，即每兩個頂點圍成了一個二角形。