凱萊圖
凱萊圖(Cayley graph)也叫做凱萊著色圖是編碼離散群的圖。它的定義是凱萊定理(以阿瑟·凱萊命名)所暗含的,并使用這個群的特定的通常有限的生成元集合。它是組合群論與幾何群論的中心工具。
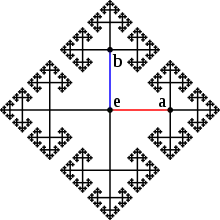
在兩個生成元a和b上的自由群的凱萊圖
定義
假設是群,而是G的生成集。凱萊圖,是如下構造的著色的有向圖。
在幾何群論中,集合,通常被假定為有限的、“對稱的”也就是,并且不包含這個群的單位元。在這種情況下,凱萊圖是正常的圖:它的邊沒有方向并且不包含環路。
例子
- 假設G = Z是無限循環群而集合S有標準生成元1和它的逆元(用加法符號為−1)構成,則它的凱萊圖是無窮鏈。
- 類似的,如果G = Zn是n階循環群而S由兩個元素構成,G的標準生成元和它的逆元,則凱萊圖是環圖Cn。
- 群的直積的凱萊圖是對應的凱萊圖的笛卡爾積。因此帶有四個元素(±1, ±1)組成的生成集的阿貝爾群Z2的凱萊圖是在平面R2上無窮網格,而帶有類似的生成集的直積Zn×Zm的凱萊圖是在環面上n乘m有限網格。
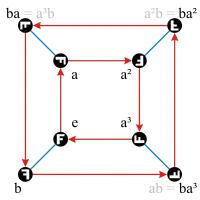
二面體群D4在兩個生成元a和b上的凱萊圖。
- 二面體群D4在兩個生成元a和b上的凱萊圖列于右側。紅色箭頭表示左乘元素a。因此元素b是自我逆轉的,表示左乘元素b藍色線是無方向的。因此這個圖是混合的:它有8個頂點,8個有向邊,4個邊。群D4的凱萊表可以從群展示得出:
- 。
特征
群通過左乘作用在自身上(參見凱萊定理)。這個作用可以看作作用在它的凱萊圖上。明顯的,一個元素映射一個頂點到頂點。凱萊圖的邊集合被這個作用所保存:邊變換成邊。任何群在自身上的左乘作用是簡單傳遞的,特別是凱萊圖是頂點傳遞的。這導致了凱萊圖的下列特征:
- 圖是群的凱萊圖,當且僅當它通過圖自同構許可的簡單傳遞作用(就是保存邊的集合)。
要從一個凱萊圖恢復群和生成集,選擇一個頂點并標記上這個群的單位元。接著對每個的頂點標記上變換到的的唯一元素。產生為凱萊圖的的生成元的集合是毗連到選擇的頂點的頂點的標記的集合。生成集合是有限(這是凱萊圖的共同假定)當且僅當這個圖是局部有限的(就是說每個頂點毗連與有限多個邊)。
Schreier陪集圖
如果轉而把頂點作為固定子群的右陪集,就得到了一個有關的構造Schreier陪集圖,它是陪集枚舉或Todd-Coxeter算法的基礎。
與群論的關係
研究圖的鄰接矩陣特別是應用譜圖理論的定理能洞察群的結構。
注釋
- Babai, L. . University of Chicago. 1996.. [2010-08-29]. (原始内容存档于2010-06-11).
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
