原群

原群並不常被研究；相對地，存在一些不同類型的原群，依據其運算需符合公理的不同。一般常被研究的原群類型有：

• 擬群－可除總是可能的非空原群；
• 環群－有單位元的擬群；
• 半群－運算為可結合的原群；
• －有單位元的半群；
• 群－有逆元的，或等價地說，可結合的環群；
• 阿貝爾群－運算為可交換的群。

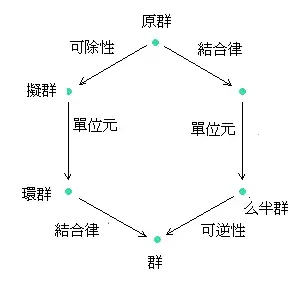
從原群到群有兩條不同的路。注意：可除性和可逆性兩者意指著消去性的存在。

原群的態射是一個函數 ${\displaystyle f:M\to N}$ ，將原群 M 映射至原群 N 上，並保留其二元運算：

${\displaystyle f(x\;*_{M}\;y)=f(x)\;*_{N}\;f(y)}$

其中的 ${\displaystyle *_{M}}$ 和 ${\displaystyle *_{N}}$ 分別代表著在 M 和 N 上的二元運算。

在一集合 X 上的自由原群 ${\displaystyle M_{X}}$ 是指由集合 X 產生出的「最一般可能的」自由原群（並沒有任何的關係或公理在產生子上；詳見自由對象）。自由原群可以用計算機科學中熟悉的詞彙來描述，如同其樹葉被 X 內的元素標示的二元樹的原群，其運算是將樹在樹根上連結。因此，自由原群在語法學中有著很基本的重要性。

自由原群有個泛性質，其內容為：若 ${\displaystyle f:X\to N}$ 是一個從集合 X 映射至任一原群 N 的函數，則會存在唯一一個 ${\displaystyle f}$ 至原群態射 ${\displaystyle f^{\prime }}$ 的擴張。其中，

${\displaystyle f^{\prime }:M_{X}\to N}$

• 自由半群
• 自由群
• 自由李群

• M. Hazewinkel, , Hazewinkel, Michiel (编), , Springer, 2001, ISBN 978-1-55608-010-4
• M. Hazewinkel, , Hazewinkel, Michiel (编), , Springer, 2001, ISBN 978-1-55608-010-4
• 埃里克·韦斯坦因. . MathWorld.