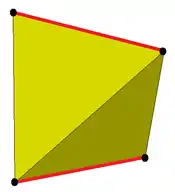
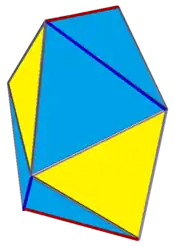
扭稜鍥形體

在幾何學中，扭稜鍥形體是指鍥形體經過扭稜變換後的像[1]，其結果為由12個正三角形面組成的凸多面體[2]，其也是除了正多面體和半正多面體的扭稜立體外，扭稜結果能以正多邊形面存在的凸多面體之一[3]。每個面都是正三角形的正扭稜鍥形體是约翰逊多面体之一，同時，由於其由三角形組成，因此也是三角面多面體之一。

異相雙三角柱
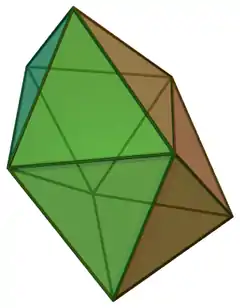(點選檢視STL骨架模型)
類別	约翰逊多面体 J₈₃ - J₈₄ - J₈₅
面	12
邊	18
頂點	8
歐拉特徵數	F=12, E=18, V=8 (χ=2)
面的種類	4+8個正三角形
頂點圖	4(3⁴) 4(3⁵)
施萊夫利符號	ss{2,4} ssr{2,2} $ss{\begin{Bmatrix}2\\2\end{Bmatrix}}$
對稱群	D_2d
參考索引	J₈₄
對偶	異相雙側柱三角柱‎
特性	凸、三角面

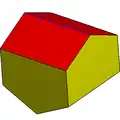異相雙側柱三角柱‎ (對偶多面體)	(展開圖)

性質

扭稜鍥形體是一種由12個三角形組成的多面體，其共有12個面、18條邊和8個頂點。扭稜鍥形體的對稱性與鍥形體相同，過其2相對邊的中點的軸為整個立體的180度旋轉對稱軸，其對稱方式為沿著軸旋轉180度會得到相同形狀，其一共包含2組這樣的對稱結構。另外一種對稱結構是沿著該軸每旋轉90度後會得到上下鏡射的形狀[4]。

根據一些理論化學的數值實驗，以扭稜鍥形體頂點為中心的球體形成的簇，在所有由八個球體構成的簇中，其兰纳-琼斯势最小[5]。

體積與表面積

面為正三角形且邊長為單位長的扭稜鍥形體，其體積為下列方程式的實數根[6][7]：

5832V^{6}-1377V^{4}-2160V^{2}-4=0

對應的扭稜鍥形體體積V約為[6]：

V\approx 0.85949

面為正三角形的扭稜鍥形體，已知扭稜鍥形體有12個正三角形面，因此其表面積A為邊長為a之正三角形面積的12倍[7]：

A=3{\sqrt {3}}a^{2}\approx 5.19615a^{2}

構造

扭稜鍥形體可以透過將鍥形體視為二角反角柱後套用扭稜變換的結果，因此扭稜鍥形體可以視為一系列扭稜反角柱無窮序列的第一項[8]。

視為二角反角柱的鍥形體其中塗上紅色的邊為對應的反角柱之底面	扭稜鍥形體（或稱為扭稜二角反角柱）

歷史

扭稜鍥形體最早由在漢斯·弗洛伊登薩和範德瓦爾登在1947年發表的論文被描述，當時該立體被稱為暹羅十二面體（Siamese dodecahedron）[9]。1964年時，約翰·德斯蒙德·伯納爾也描述了相同的形狀，並將其命名為三角十二面體（dodecadeltahedron）代表其為具有12個面的三角面多面體[10]，雖然仍然存在其他12個面的三角面單純多面體，如雙六角錐，然而只有扭稜鍥形體可以在所有面都是正三角形的情況下保持凸多面體且不退化的狀態。約翰·德斯蒙德·伯納爾對密接球體堆砌所形成的空隙之形狀感興趣，因此他對三角面多面體提出了更嚴格的定義，其定義為：三角面多面體是一個由三角形面組成的凸多面體，其可以透過全等球體的集合的中心構成，其切線代表多面體的邊，且這組球體包住的中間空隙區域只有一個，且沒有足夠的空間再放入一個全等的球體。例如雙三角錐會被此種定義排除，因為其會形成2個四面體形狀的孔隙，而非只有一個孔隙、雙五角錐也會被此種定義排除，因為置於雙五角錐頂點上的球體會互相重合而無法構成球堆砌、正二十面體也會被此種定義排除，因為將球體置於正二十面體頂點所形成的球堆砌之中心空隙還有足夠的空間容納下另一顆球。伯納爾認為扭稜鍥形體這種形狀在晶體學中是鈣離子非常常見的配位。[10]

1966年诺曼·约翰逊將92種由正多邊形組成的不是正多面體也不是半正多面體的立體命名並給予描述，其中包括了扭稜鍥形體。[11] 在後續的研究中，不同的學者也有依據其外觀和其他立體的關聯給予不同的名稱，例如其外觀與雙五角錐類似，因此又被稱為變稜雙五角錐或變形雙五角錐（）[12]。對於扭稜鍥形體的對偶多面體亦存在相關研究[13]。2017年時戈柏學者等人發現扭稜鍥形體的對偶多面體是一種空間填充多面體[14]。

參見

扭稜四面體

參考文獻

Finbow, Arthur S.; Hartnell, Bert L.; Nowakowski, Richard J.; Plummer, Michael D., , Discrete Applied Mathematics, 2010, 158 (8): 894–912, MR 2602814, doi:10.1016/j.dam.2009.08.002.

. eusebeia. [2019-09-28]. （原始内容存档于2019-09-28）.
Montroll, J. . Dover Origami Papercraft Series. Dover Publications. 2004: 38. ISBN 9780486439587. LCCN 2004056139.
Arvo, J. . Graphics Gems - IBM. Elsevier Science. 2013: 178. ISBN 9780080507545.
Cundy, H. Martyn, , The Mathematical Gazette, 1952, 36: 263–266, MR 0051525, doi:10.2307/3608204
Sloane, N. J. A.; Hardin, R. H.; Duff, T. D. S.; Conway, J. H., , Discrete and Computational Geometry, 1995, 14 (3): 237–259, MR 1344734, doi:10.1007/BF02570704.
David I. McCooey. . dmccooey.com. 2015 [2019-09-28]. （原始内容存档于2019-09-28）.
{{Cite web |url=http://mathworld.wolfram.com/SnubDisphenoid.html |title=Snub Disphenoid |website=at MathWorld--A Wolfram Web Resource |publisher=Wolfram Research, Inc. |editor-first=Eric W. |editor-last=Weisstein |editor-link=埃里克·韦斯坦因 |accessdate= |quote= |language=en }}
Jim McNeill. . orchidpalms.com. [2019-09-28]. （原始内容存档于2019-03-27）.
Freudenthal, H.; van d. Waerden, B. L., , Simon Stevin, 1947, 25: 115–121, MR 0021687.
Bernal, J. D., , Proceedings of the Royal Society of London, Series A, Mathematical and Physical Sciences, 1964, 280 (1382): 299–322, JSTOR 2415872
Johnson, Norman W., , Canadian Journal of Mathematics, 1966, 18: 169–200, MR 0185507, Zbl 0132.14603, doi:10.4153/cjm-1966-021-8.
鶴田直也, (PDF), 筑波大学, 2015 [2019-09-28], （原始内容存档 (PDF)于2019-02-18）
Convex regular-faced polyhedra with conditional edges 页面存档备份，存于 P3,2
Goldberg, Michael, On the space-filling octahedra, Geometriae Dedicata, January 1981, Volume 10, Issue 1, pp 323–335 页面存档备份，存于 PDF 的存檔，存档日期2017-12-22.

外部链接

埃里克·韦斯坦因, 扭稜鍥形體（參閱詹森多面體）於MathWorld（英文）

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] . eusebeia. [2019-09-28]. （原始内容存档于2019-09-28）.

[book_montroll2004constellation-2] Montroll, J. . Dover Origami Papercraft Series. Dover Publications. 2004: 38. ISBN 9780486439587. LCCN 2004056139.

[book_arvo2013graphics-3] Arvo, J. . Graphics Gems - IBM. Elsevier Science. 2013: 178. ISBN 9780080507545.

[4] Cundy, H. Martyn, , The Mathematical Gazette, 1952, 36: 263–266, MR 0051525, doi:10.2307/3608204

[shdc-5] Sloane, N. J. A.; Hardin, R. H.; Duff, T. D. S.; Conway, J. H., , Discrete and Computational Geometry, 1995, 14 (3): 237–259, MR 1344734, doi:10.1007/BF02570704.

[dmccooey_DisdyakisDodecahedron-6] David I. McCooey. . dmccooey.com. 2015 [2019-09-28]. （原始内容存档于2019-09-28）.

[mathworld_SnubDisphenoid-7] {{Cite web |url=http://mathworld.wolfram.com/SnubDisphenoid.html |title=Snub Disphenoid |website=at MathWorld--A Wolfram Web Resource |publisher=Wolfram Research, Inc. |editor-first=Eric W. |editor-last=Weisstein |editor-link=埃里克·韦斯坦因 |accessdate= |quote= |language=en }}

[8] Jim McNeill. . orchidpalms.com. [2019-09-28]. （原始内容存档于2019-03-27）.

[9] Freudenthal, H.; van d. Waerden, B. L., , Simon Stevin, 1947, 25: 115–121, MR 0021687.

[Bernal_1964-10] Bernal, J. D., , Proceedings of the Royal Society of London, Series A, Mathematical and Physical Sciences, 1964, 280 (1382): 299–322, JSTOR 2415872

[11] Johnson, Norman W., , Canadian Journal of Mathematics, 1966, 18: 169–200, MR 0185507, Zbl 0132.14603, doi:10.4153/cjm-1966-021-8.

[phdthesis_鶴田直也2015折紙の幾何的な制約を考慮した形状設計に関する研究-12] 鶴田直也, (PDF), 筑波大学, 2015 [2019-09-28], （原始内容存档 (PDF)于2019-02-18）

[13] Convex regular-faced polyhedra with conditional edges 页面存档备份，存于 P3,2

[14] Goldberg, Michael, On the space-filling octahedra, Geometriae Dedicata, January 1981, Volume 10, Issue 1, pp 323–335 页面存档备份，存于 PDF 的存檔，存档日期2017-12-22.