调和矩阵

在图论中，调和矩阵（harmonic matrix），也称拉普拉斯矩阵或拉氏矩阵（laplacian matrix）、离散拉普拉斯（discrete laplacian），是图的矩阵表示。[1]

调和矩阵也是拉普拉斯算子的离散化。换句话说，调和矩阵的缩放极限是拉普拉斯算子。它在机器学习和物理学中有很多应用。

定义

若G是单纯图，G有n个顶点，A是邻接矩阵，D是度数矩阵，则调和矩阵是[1]

$L=D-A$

$L_{i,j}:={\begin{cases}\deg(v_{i})&{\mbox{if}}\ i=j\\-1&{\mbox{if}}\ i\neq j\ {\mbox{and}}\ v_{i}{\mbox{ is adjacent to }}v_{j}\\0&{\mbox{otherwise}}\end{cases}}$

动机

这跟拉普拉斯算子有什么关系？若f 是加权图G的顶点函数，则[2]

$E(f)=\sum w(uv)(f(u)-f(v))^{2}/2=f^{t}Lf$

w是边的权重函数。u、v是顶点。f = (f(1), ..., f(n)) 是n维的矢量。上面泛函也称为Dirichlet泛函。[3]

接续矩阵

而且若K是接续矩阵（incidence matrix），则[2]

$K_{ev}=\left\{{\begin{array}{rl}1,&{\text{if }}v=i\\-1,&{\text{if }}v=j\\0,&{\text{otherwise}}.\end{array}}\right.$

$L=K^{t}K$

Kf 是f 的图梯度。另外，特征值满足

${\begin{aligned}\lambda _{i}&=\mathbf {v} _{i}^{\textsf {T}}L\mathbf {v} _{i}\\&=\mathbf {v} _{i}^{\textsf {T}}M^{\textsf {T}}M\mathbf {v} _{i}\\&=\left(M\mathbf {v} _{i}\right)^{\textsf {T}}\left(M\mathbf {v} _{i}\right)\\\end{aligned}}$

举例

图	度数矩阵	邻接矩阵	调和矩阵
	${\textstyle \left({\begin{array}{rrrrrr}2&0&0&0&0&0\\0&3&0&0&0&0\\0&0&2&0&0&0\\0&0&0&3&0&0\\0&0&0&0&3&0\\0&0&0&0&0&1\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrrrrr}0&1&0&0&1&0\\1&0&1&0&1&0\\0&1&0&1&0&0\\0&0&1&0&1&1\\1&1&0&1&0&0\\0&0&0&1&0&0\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrrrrr}2&-1&0&0&-1&0\\-1&3&-1&0&-1&0\\0&-1&2&-1&0&0\\0&0&-1&3&-1&-1\\-1&-1&0&-1&3&0\\0&0&0&-1&0&1\\\end{array}}\right)}$

其他形式

対称正規化调和矩阵

$L^{\text{sym}}:=D^{-{\frac {1}{2}}}LD^{-{\frac {1}{2}}}=I-D^{-{\frac {1}{2}}}AD^{-{\frac {1}{2}}}$

$L_{i,j}^{\text{sym}}:={\begin{cases}1&{\mbox{if }}i=j{\mbox{ and }}\deg(v_{i})\neq 0\\-{\frac {1}{\sqrt {\deg(v_{i})\deg(v_{j})}}}&{\mbox{if }}i\neq j{\mbox{ and }}v_{i}{\mbox{ is adjacent to }}v_{j}\\0&{\mbox{otherwise}}.\end{cases}}$

注意[4]

$\lambda \ =\ {\frac {\langle g,L^{\text{sym}}g\rangle }{\langle g,g\rangle }}\ =\ {\frac {\left\langle g,D^{-{\frac {1}{2}}}LD^{-{\frac {1}{2}}}g\right\rangle }{\langle g,g\rangle }}\ =\ {\frac {\langle f,Lf\rangle }{\left\langle D^{\frac {1}{2}}f,D^{\frac {1}{2}}f\right\rangle }}\ =\ {\frac {\sum _{u\sim v}(f(u)-f(v))^{2}}{\sum _{v}f(v)^{2}d_{v}}}\ \geq \ 0,$

随机漫步

$L^{\text{rw}}:=D^{-1}L=I-D^{-1}A$

$L_{i,j}^{\text{rw}}:={\begin{cases}1&{\mbox{if }}i=j{\mbox{ and }}\deg(v_{i})\neq 0\\-{\frac {1}{\deg(v_{i})}}&{\mbox{if }}i\neq j{\mbox{ and }}v_{i}{\mbox{ is adjacent to }}v_{j}\\0&{\mbox{otherwise}}.\end{cases}}$

动力学和微分方程

例如，离散的冷却定律使用调和矩阵[5]

${\begin{aligned}{\frac {d\phi _{i}}{dt}}&=-k\sum _{j}A_{ij}\left(\phi _{i}-\phi _{j}\right)\\&=-k\left(\phi _{i}\sum _{j}A_{ij}-\sum _{j}A_{ij}\phi _{j}\right)\\&=-k\left(\phi _{i}\ \deg(v_{i})-\sum _{j}A_{ij}\phi _{j}\right)\\&=-k\sum _{j}\left(\delta _{ij}\ \deg(v_{i})-A_{ij}\right)\phi _{j}\\&=-k\sum _{j}\left(\ell _{ij}\right)\phi _{j}.\end{aligned}}$

使用矩阵矢量

${\begin{aligned}{\frac {d\phi }{dt}}&=-k(D-A)\phi \\&=-kL\phi \end{aligned}}$

${\frac {d\phi }{dt}}+kL\phi =0$

解是

${\begin{aligned}{\frac {d\left(\sum _{i}c_{i}\mathbf {v} _{i}\right)}{dt}}+kL\left(\sum _{i}c_{i}\mathbf {v} _{i}\right)&=0\\\sum _{i}\left[{\frac {dc_{i}}{dt}}\mathbf {v} _{i}+kc_{i}L\mathbf {v} _{i}\right]&=\\\sum _{i}\left[{\frac {dc_{i}}{dt}}\mathbf {v} _{i}+kc_{i}\lambda _{i}\mathbf {v} _{i}\right]&=\\{\frac {dc_{i}}{dt}}+k\lambda _{i}c_{i}&=0\\\end{aligned}}$

$c_{i}(t)=c_{i}(0)e^{-k\lambda _{i}t}$

$c_{i}(0)=\left\langle \phi (0),\mathbf {v} _{i}\right\rangle$

平衡举动

当 ${\textstyle \lim _{t\to \infty }\phi (t)}$ 的时候，

$\lim _{t\to \infty }e^{-k\lambda _{i}t}=\left\{{\begin{array}{rlr}0&{\text{if}}&\lambda _{i}>0\\1&{\text{if}}&\lambda _{i}=0\end{array}}\right\}$

$\lim _{t\to \infty }\phi (t)=\left\langle c(0),\mathbf {v^{1}} \right\rangle \mathbf {v^{1}}$

$\mathbf {v^{1}} ={\frac {1}{\sqrt {N}}}[1,1,...,1]$

$\lim _{t\to \infty }\phi _{j}(t)={\frac {1}{N}}\sum _{i=1}^{N}c_{i}(0)$

MATLAB代码

N = 20;%The number of pixels along a dimension of the image
A = zeros(N, N);%The image
Adj = zeros(N*N, N*N);%The adjacency matrix

%Use 8 neighbors, and fill in the adjacency matrix
dx = [-1, 0, 1, -1, 1, -1, 0, 1];
dy = [-1, -1, -1, 0, 0, 1, 1, 1];
for x = 1:N
   for y = 1:N
       index = (x-1)*N + y;
       for ne = 1:length(dx)
           newx = x + dx(ne);
           newy = y + dy(ne);
           if newx > 0 && newx <= N && newy > 0 && newy <= N
               index2 = (newx-1)*N + newy;
               Adj(index, index2) = 1;
           end
       end
   end
end

%%%BELOW IS THE KEY CODE THAT COMPUTES THE SOLUTION TO THE DIFFERENTIAL
%%%EQUATION
Deg = diag(sum(Adj, 2));%Compute the degree matrix
L = Deg - Adj;%Compute the laplacian matrix in terms of the degree and adjacency matrices
[V, D] = eig(L);%Compute the eigenvalues/vectors of the laplacian matrix
D = diag(D);

%Initial condition (place a few large positive values around and
%make everything else zero)
C0 = zeros(N, N);
C0(2:5, 2:5) = 5;
C0(10:15, 10:15) = 10;
C0(2:5, 8:13) = 7;
C0 = C0(:);

C0V = V'*C0;%Transform the initial condition into the coordinate system 
%of the eigenvectors
for t = 0:0.05:5
   %Loop through times and decay each initial component
   Phi = C0V.*exp(-D*t);%Exponential decay for each component
   Phi = V*Phi;%Transform from eigenvector coordinate system to original coordinate system
   Phi = reshape(Phi, N, N);
   %Display the results and write to GIF file
   imagesc(Phi);
   caxis([0, 10]);
   title(sprintf('Diffusion t = %3f', t));
   frame = getframe(1);
   im = frame2im(frame);
   [imind, cm] = rgb2ind(im, 256);
   if t == 0
      imwrite(imind, cm, 'out.gif', 'gif', 'Loopcount', inf, 'DelayTime', 0.1); 
   else
      imwrite(imind, cm, 'out.gif', 'gif', 'WriteMode', 'append', 'DelayTime', 0.1);
   end
end

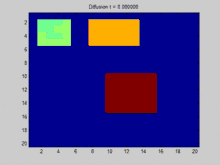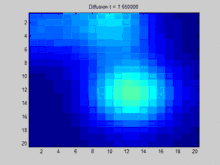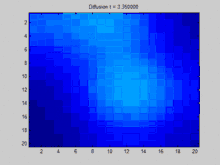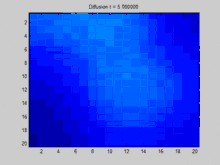
GIF：离散拉普拉斯过程，使用拉普拉斯矩阵

应用

Kirchoff定理曰：调和矩阵的行列式
人工智能
非线性降维
Spectral clustering
Cheeger不等式曰：调和矩阵的第二大的特征值跟最大割問題有关
图Signal processing[3]

参考文献

Weisstein, Eric W. . mathworld.wolfram.com. [2020-02-14]. （原始内容存档于2019-12-23）（英语）.
. www.quora.com. [2020-02-14].
Shuman, David I.; Narang, Sunil K.; Frossard, Pascal; Ortega, Antonio; Vandergheynst, Pierre. . IEEE Signal Processing Magazine. 2013-05, 30 (3): 83–98 [2020-02-14]. ISSN 1053-5888. doi:10.1109/MSP.2012.2235192. （原始内容存档于2020-01-11）.
Chung, Fan. . American Mathematical Society. 1997 [1992] [2020-02-14]. ISBN 978-0821803158. （原始内容存档于2020-02-14）.
Newman, Mark. . Oxford University Press. 2010. ISBN 978-0199206650.

阅读

T. Sunada. . P. Exner, J. P. Keating, P. Kuchment, T. Sunada, A. Teplyaev (编). 77. 2008: 51–86. ISBN 978-0-8218-4471-7.
B. Bollobás, Modern Graph Theory, Springer-Verlag (1998, corrected ed. 2013), ISBN 0-387-98488-7, Chapters II.3 (Vector Spaces and Matrices Associated with Graphs), VIII.2 (The Adjacency Matrix and the Laplacian), IX.2 (Electrical Networks and Random Walks).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[:0-1] Weisstein, Eric W. . mathworld.wolfram.com. [2020-02-14]. （原始内容存档于2019-12-23）（英语）.

[:1-2] . www.quora.com. [2020-02-14].

[:2-3] Shuman, David I.; Narang, Sunil K.; Frossard, Pascal; Ortega, Antonio; Vandergheynst, Pierre. . IEEE Signal Processing Magazine. 2013-05, 30 (3): 83–98 [2020-02-14]. ISSN 1053-5888. doi:10.1109/MSP.2012.2235192. （原始内容存档于2020-01-11）.

[4] Chung, Fan. . American Mathematical Society. 1997 [1992] [2020-02-14]. ISBN 978-0821803158. （原始内容存档于2020-02-14）.

[5] Newman, Mark. . Oxford University Press. 2010. ISBN 978-0199206650.