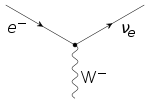
輕子
輕子(Lepton)是一種不参與强相互作用、自旋为1/2的基本粒子。[1]電子是最為人知的一種輕子;大部分化學領域都會涉及到與電子的相互作用,原子不能沒有它,所有化學性質都直接與它有關。輕子又分為兩類:「帶電輕子」與「中性輕子」。帶電輕子包括電子、緲子、陶子,可以與其它粒子組合成複合粒子,例如原子、電子偶素等等。 在所有帶電輕子中,電子的質量最輕,也是宇宙中最穩定、最常見的輕子;質量較重的緲子與陶子會很快地衰變成電子,緲子與陶子必須經過高能量碰撞製成,例如使用粒子加速器或在宇宙線探測實驗。中性輕子包括電中微子、緲中微子、陶中微子;它們很少與任何粒子相互作用,很難被觀測到。
 | |
| 组成 | 基本粒子 |
|---|---|
| 系 | 费米-狄拉克 |
| 代 | 第一代、第二代、第三代 |
| 基本相互作用 | 電磁、引力、弱 |
| 符号 | l |
| 反粒子 | 反輕子 (l) |
| 类型 | 6 (電子、電中微子、緲子、緲中微子、陶子、陶中微子) |
| 电荷 | +1 e、0 e、−1 e |
| 色荷 | No |
| 自旋 | 1⁄2 |
輕子一共有六種風味,形成三個世代。[2]第一代是電輕子,包括電子(e−
)與電中微子 (ν
e)。第二代是緲輕子,包括緲子(μ−
)與緲中微子 (ν
μ)。第三代是陶輕子,包括陶子(τ−
)與陶中微子(ν
τ)。
輕子擁有很多內秉性質,包括電荷、自旋、質量等等。輕子與夸克有一點很不相同:輕子不會感受到強作用力。輕子會感受到其它三種基礎力:引力、弱作用力、電磁力。但是,由於中微子的電性是中性,中微子不會感受到電磁力。每一種輕子風味都有其對應的反粒子,稱為「反輕子」。帶電輕子與對應的反輕子唯一不同之處是帶有電荷的正負號相反。根據某些理論,中微子是自己的反粒子,但這論點尚未被證實。
在標準模型裏,輕子扮演重要角色,電子是原子的成分之一,與質子、中子共同組成原子。在某些被合成的奇異原子裏,電子被更換為緲子或陶子。像電子偶素一類的輕子-反輕子粒子也可以被合成。
詞源學
英文術語「lepton」源自希臘語「」(leptón),是「」(leptós)的中性,含意為"小、薄"。[3]萊昂·羅森菲爾德於1948年最先為英文術語「lepton」命名。 [4]
在克理斯蒂安·莫勒教授的建議之後,決定用「lepton」(從「λεπτός」,小、薄)這字來稱呼一種小質量的粒子。
這命名不正確地假定所有輕子的質量都很小。在洛森斐命名那時,學術界只知道有電子與緲子兩種輕子。它們的質量的確很小,電子的質量為0.511 MeV,[5]緲子的質量為105.7 MeV,[6]比質子的質量938.3 MeV輕很多[7]。可是,在1970年代中期發現的陶子,它的質量是1777 MeV[8],幾乎是質子的兩倍。
歷史

最先被辨識的輕子是電子,英國物理學者約瑟夫·湯姆森與實驗團隊於1897年發現電子。[9] [10]1930年,沃爾夫岡·包立大膽假設電中微子存在,這是為了解釋β衰變的能量缺失問題,挽救能量守恆定律;包立認為,所有最初與最終觀察到的粒子的能量差,都被一種尚未探測到的粒子帶走了,這粒子具有電中性,不會留下軌跡,所以很難探測到。[11][12]三年後,恩里科·費米給出理論,成功描述β衰變,強力支持包立的假設。費米將這粒子命名為「中微子」,意思為「微小的中子」。在那時期,電中微子被稱為中微子,因為尚未發現其它世代的中微子。1956年,克萊德·科溫與弗雷德里克·萊因斯共同完成科溫-萊因斯中微子實驗首先直接觀察到中微子的存在。[12][13]
在電子被發現大約40年之後,卡爾·安德森於1936年發現了緲子。由於它的質量,緲子最初被歸類為介子,而不是輕子。[14]漸漸地,學者發覺緲子的性質更接近電子,只是質量比較大,而且緲子不會感受到強相對作用,不具有介子的性質。1947年,才有學者開始提議一群粒子被歸類為輕子的概念。[12] 後來,緲子被重新歸類,緲子、電子與電中微子一起被歸類為輕子。1962年 利昂·萊德曼、梅爾文·施瓦茨與傑克·施泰因貝格爾做實驗直接探測到緲中微子,證實不只一種中微子存在。[15]
馬丁·佩爾與他的實驗團隊於1975年完成實驗首先探測到陶子。[16]如同電子與緲子,物理學者認為它應該也有伴隨的中微子,這是因為他們觀察到類似β衰變的缺失能量問題。費米實驗室的直接觀察陶中微子實驗(Direct Observation of the NU Tau,DONUT )團隊於2000年探測到陶中微子參與作用的證據。[17]
虽然現有數據符合三個世代的輕子,有些粒子物理學者仍在尋找第四代帶電輕子。這種帶電輕子的質量下限為100.8 GeV,[18]伴隨它的中微子最少應該帶有質量45.0 GeV。[19]
性質
自旋與手徵性

輕子是自旋1⁄2粒子,只能處於兩種自旋態:上旋或下旋。自旋統計定理將它們按照自旋歸類為費米子,遵守包立不相容原理,因此任何兩個全同的輕子不能同時佔有相同的量子態。[20]:28-29
手徵性與螺旋性(helicity)是與自旋緊密相關的兩種性質,螺旋性跟粒子的自旋與動量之間的相對方向有關;假若是同向,則粒子具有右手螺旋性,否則粒子具有左手螺旋性。對於不帶質量粒子,這相對方向與參考系無關,可是,對於帶質量粒子,由於可以藉著洛倫茲變換來改換參考系,從不同的參考系觀察,粒子動量不同,因此翻改螺旋性,可以從右手螺旋性翻改為左手螺旋性,或從左手螺旋性翻改為右手螺旋性。手徵性是通過龐加萊群(Poincaré group)的變換來定義的性質。對於不帶質量粒子,手徵性與螺旋性一致;對於帶質量粒子,手徵性與螺旋性有別。[21]:137-138, 338-340
在很多量子場論裏,例如量子電動力學與量子色動力學,並沒有對左手與右手費米子作任何區分,可是,在標準模型的弱相互作用理論裏,按照手徵性區分的左手與右手費米子被非對稱地處理,只有左手費米子參與弱相互作用,右手中微子不存在。這是宇稱違反的典型例子。[21]:ch 9.7
電磁相互作用
輕子的電荷決定了它所產生的電磁場,也決定了它怎樣響應外電磁場。輕子的每個世代的組員都有一個帶電輕子與一個中性輕子,例如,第一代輕子為電子e−
與電中微子ν
e。
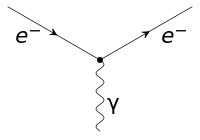
使用量子場論的語言,帶電輕子所涉及的電磁相互作用表達為這輕子與電磁場的量子(光子)彼此之間的相互作用。右圖是電子-光子相互作用的費曼圖。
由於輕子具有自旋,帶電輕子會產生磁場,磁偶極矩為
- ;
其中,是輕子的質量,是輕子的g-因數(g-factor)。
一階近似量子力學預測,對於所有輕子,g-因數為2;可是高階量子效應,因為費曼圖裏的虛粒子圈對於這數字給出修正。這些修正,稱為反常磁偶極矩(anomalous magnetic dipole moment),對於量子場論模型的細節非常敏感,因此是準確檢驗標準模型的好機會。對於電子測量其反常磁偶極矩所得到的實驗數值符合理論結果至8個有效數字。[22]:197
弱相互作用
| ||||||
在標準模型裏,輕子可以按照手徵性分為左手輕子與右手輕子;左手輕子的弱同位旋T為1⁄2,左手帶電輕子與左手中微子的弱同位旋投影(弱同位旋的第三分量)T3分別為-1⁄2、+1⁄2,弱相互作用是由它們組成二重態(doublet state)(ν
eL, e−
L)共同實現;右手帶電輕子的弱同位旋T為0,形成單態,不參與弱相互作用;右手中微子並不存在。[21]:342-344
希格斯機制將弱同位旋SU(2)與弱超荷U(1)對稱的四個規範場,重新組合成傳遞弱相對作用的三個帶質量玻色子 (W+
、W−
、Z0
)與傳遞電磁相對作用的不帶質量玻色子(光子)。通過蓋爾曼-西島方程,可以從弱同位旋投影T3與弱超荷YW計算出電荷Q:
- 。
為了符合觀察到的任何粒子所帶有的電荷,所有左手弱同位旋二重態(ν
eL, e−
L)的弱超荷YW必須為-1,而右手弱同位旋單態(e−
R)}的弱超荷YW必須為-2。
質量
在標準模型裏,每一個輕子原本不具有內秉質量;通過與希格斯場耦合,帶電輕子獲得有效質量,但中微子仍舊不帶質量,這意味著不同世代的帶電輕子不會相互混合,與夸克的物理行為大不相同。這結果符合當今實驗數據。[22]:27
但是,從實驗中得知(最顯著的是中微子振盪實驗),[23]中微子實際帶有微小質量,大約小於2 eV。[24]這意味著後標準模型 (beyond the Standard Model)的物理現象。當今最被物理學者青睞的理論延伸是翹翹板機制,它可以解釋為甚麼左手中微子的質量遠輕於對應的帶電輕子,為甚麼做實驗尚未能觀察到任何右手中微子。
輕子數
每一代輕子的成員組成一個弱同位旋二重態:
- 、、。
每一代弱同位旋二重態的成員都被分派一個輕子數。在標準模型裏,輕子數守恆。[25]:27-49電子與電中微子的電子數Le為1。緲子與緲中微子的緲子數Lμ為1。陶子與陶中微子的陶子數Lτ為1。 反輕子的輕子數為對應輕子的輕子數乘以−1。
輕子數守恆的意思就是同類氫子數的代數和保持不變,當粒子耦合時;這意味著只有同一代的輕子與反輕子才能成對產生。例如,以下過程是被允許的:
以下過程是不被允許的:
但是,中微子振盪違反單獨輕子數守恆,這是後標準模型物理的確鑿證據。更強的守恆定律是總輕子數守恆。中微子振盪遵守總輕子數守恆。但是,手徵反常稍微違反了這守恆定律。
普適性
輕子與對應的中微子之間的相互作用與風味無關,換句話說,對於電子與電中微子之間的相互作用、緲子與緲中微子之間的相互作用、陶子與陶中微子之間的相互作用,假若將質量差別納入考量,則這三種相互作用的效應相等。這性質稱為輕子相互作用的「普適性」。所有已知實驗數據與這種普適性一致[25]:36-38做實驗測量陶子與緲子的平均壽命,或Z玻色子衰變為輕子的部分衰變寬度,可以檢驗這性質。在大型正负电子对撞机與史丹福直線加速器裏,完成了很多這類檢驗普適性的實驗。[26]:241-243[27]:138
對於過程μ−
→ e−
+ ν
e
+ ν
μ
,緲子的衰變率以方程式表示為(更詳盡內容,請參閱緲子衰變)[25]:36-38
- ;
其中,是常數,是費米耦合常數,是緲子的質量。
對於過程τ−
→ e−
+ ν
e
+ ν
τ
,陶子的衰變率以同樣形式的方程式表示為
- ;
其中,是常數,是陶子的質量。
緲子-陶子普適性意味著。普適性也能夠解釋緲子壽命與陶子壽命之間的關係。輕子的壽命與衰變率之間的關係為
- ;
其中,與分別標記過程的分支比與共振寬度。
陶子與緲子的壽命比因此為
- 。
從實驗獲得的緲子分支比與陶子分支比,可以計算出壽命比為大約1.328×10−7,實驗測量得到的壽命比為 ~1.323×10−7。兩者之差異是因為、實際並不是常數,它們與輕子的質量有關。
另外,由於電子-緲子普適性,陶子衰變為電子的分支比(17.85%) 與衰變為緲子的分支比 (17.36%) 相同(在誤差範圍內):[8]
- 。
輕子列表
| 粒子/反粒子名字 | 符號 | 電荷 (e) | 自旋 | Le | Lμ | Lτ | 質量(MeV) | 壽命 (秒) | 通常衰變 |
|---|---|---|---|---|---|---|---|---|---|
| 電子 / 正子[5] | e− /e+ |
−1/+1 | 1⁄2 | +1/−1 | 0 | 0 | 0.510998910(13) | 穩定 | 穩定 |
| 緲子 / 反緲子[6] | μ− /μ+ |
−1/+1 | 1⁄2 | 0 | +1/−1 | 0 | 105.6583668(38) | 2.197019(21)×10−6 | e− + ν e + ν μ |
| 陶子 / 反陶子[8] | τ− /τ+ |
−1/+1 | 1⁄2 | 0 | 0 | +1/−1 | 1776.84(17) | 2.906(10)×10−13 | http://pdg.lbl.gov/2008/listings/s035.pdf 页面存档备份,存于 |
| 電中微子 / 反電中微子[24] | ν e /ν e |
0 | 1⁄2 | +1/−1 | 0 | 0 | < 0.0000022[28] | 未知 | |
| 緲中微子 / 反緲中微子[24] | ν μ /ν μ |
0 | 1⁄2 | 0 | +1/−1 | 0 | < 0.17[28] | 未知 | |
| 陶中微子 / 反陶中微子[24] | ν τ /ν τ |
0 | 1⁄2 | 0 | 0 | +1/−1 | < 15.5[28] | 未知 |
參考文獻
- . Encyclopædia Britannica. [2010-09-29]. (原始内容存档于2015-05-11).
- R. Nave. . HyperPhysics. Georgia State University, Department of Physics and Astronomy. [2010-09-29]. (原始内容存档于2015-04-02).
- . Liddell, Henry George; Scott, Robert; A Greek–English Lexicon at the Perseus Project。
- L. Rosenfeld (1948)
- C. Amsler et al. (2008): 页面存档备份,存于 Particle listings – e−
- C. Amsler et al. (2008): 页面存档备份,存于 Particle listings – μ−
- C. Amsler et al. (2008): 页面存档备份,存于 Particle listings – p+
- C. Amsler et al. (2008): 页面存档备份,存于 Particle listings – τ−
- S. Weinberg. . Cambridge University Press. 2003. ISBN 0-521-82351-X.
- R. Wilson. . CRC Press. 1997: 138. ISBN 0-7484-0748-0.
- K. Riesselmann. . Symmetry Magazine. 2007, 4 (2).
- (PDF). Los Alamos Science. 1997, 25: 3 [2010-02-10]. (原始内容存档 (PDF)于2013-02-21).
- F. Reines, C.L. Cowan, Jr.; Cowan. . Nature. 1956, 178 (4531): 446. Bibcode:1956Natur.178..446R. doi:10.1038/178446a0.
- S.H. Neddermeyer, C.D. Anderson; Anderson. . Physical Review. 1937, 51 (10): 884–886. Bibcode:1937PhRv...51..884N. doi:10.1103/PhysRev.51.884.
- I.V. Anicin. . SFIN (Institute of Physics, Belgrade) year XV, Series A: Conferences, No. A2 (2002) 3–59. 2005: 3172. Bibcode:2005physics...3172A. arXiv:physics/0503172.
- M.L. Perl; 等. . Physical Review Letters. 1975, 35 (22): 1489–1492. Bibcode:1975PhRvL..35.1489P. doi:10.1103/PhysRevLett.35.1489.
- K. Kodama et al. (DONUT Collaboration). . Physics Letters B. 2001, 504 (3): 218. Bibcode:2001PhLB..504..218D. arXiv:hep-ex/0012035. doi:10.1016/S0370-2693(01)00307-0.
- C. Amsler et al. (2008) Heavy Charged Leptons Searches 页面存档备份,存于
- C. Amsler et al. (2008) Searches for Heavy Neutral Leptons 页面存档备份,存于
- Mark Srednicki. . Cambridge University Press. 25 January 2007 [2014-08-01]. ISBN 978-1-139-46276-1. (原始内容存档于2011-07-25).
- Griffiths, David J., 2nd revised, WILEY-VCH, 2008, ISBN 978-3-527-40601-2
- Peskin, Michael; Schroeder, Daniel. Reprint. Westview Press. 1995. ISBN 978-0201503975.
- Y.Fukuda; 等. . Physical Review Letters. 1998, 81 (8): 1562–1567. Bibcode:1998PhRvL..81.1562F. arXiv:hep-ex/9807003. doi:10.1103/PhysRevLett.81.1562.
- C.Amsler et al. (2008): Particle listings – Neutrino properties 页面存档备份,存于
- B.R. Martin, G. Shaw. . . John Wiley & Sons. 2008. ISBN 0470032944.
- J. P. Cumalat. . Atlantica Séguier Frontières. 1993. ISBN 978-2-86332-129-4.
- G Fraser. . CRC Press. 1 January 1998. ISBN 978-1-4200-5033-2.
- J. Peltoniemi, J. Sarkamo (2005)