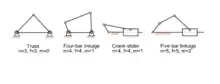
连杆机构
连杆机构(mechanical linkage)是由許多构件組成,用來傳遞力及運動的机械結构。會假設各構件為剛體[1]。可以用幾何學的方式分析構件的運動,構件和構件之間的連接可能是純移動、純轉動或是滑動,一般會稱為機械連接(joint)。若連桿是用剛性的構件以及理想的機械連接來模擬,會稱為是運動鏈。
.jpg.webp)

连杆机构可以用開放鏈(其幾何形狀無法形成封閉曲線)、封閉鏈(其幾何形狀可形成封閉曲線)組成,也可以兩者都用。每一個構件都是透過機械連接連接到一個或是多個構件。因此運動鏈也可以繪成由邊和頂點組成的圖,其中的構件為邊,機械連接為頂點,稱為连杆圖(linkage graph)。
理想機械連接的運動會和歐氏位移群中的子群有關。子群的數量稱為是機械連接的自由度。连杆机构一般會設計將給定的輸入力以及位移轉換為想要的輸出力以及位移。輸出力和輸入力的比例稱為连杆机构的機械利益,而輸入速度和輸出速度的比例稱為速度比。理想连杆的機械利益會等於速度比。
運動鏈中若有一個構件是固定不動的,此運動鏈會稱為是機構(mechanism),若连杆机构是設計為固定不動的,會稱為是結構(structure)。
應用
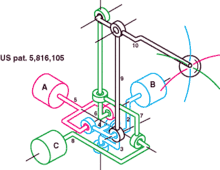
槓桿應該是最簡單的連桿,槓桿的樞紐位在支點上,支點是在固定點(或地面)上。若槓桿受力旋轉,離支點較遠的點速度會比離支點較近的點要快。輸入旳功等於輸出的功,因此在離支點較遠的位置施較小的力,會等於在離支點較近的位置施較大的力。輸出力和輸入力的比例稱為機械利益。
若二個杆件分別有一端有樞紐,分別固定在固定點上,二杆件的另一端連接到同一杆件的兩端,此機構稱為四杆机构,二個有樞紐,接到固定點的桿件稱為曲柄,連接二曲柄的為結合桿(coupler)。
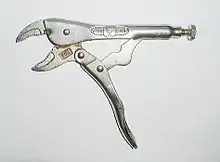
连杆是机器及工具中重要的零件,四連杆的例子有可以將力放大的斷線鉗、車輛中的懸吊系統、機器手臂以及行走機器人裡面的複雜連桿機構。内燃机使用滑塊—曲柄的四連杆,由活塞、連桿及曲轴組成,可以將氣體膨脹及收縮產生的功轉換為旋轉的功。許多簡單的連桿可以進行複雜的功能。
其他比較特殊的连杆例子有雨刷、自行車懸吊系統、行走機器人的腿形機構,以及重型動力機械的液壓缸。在這些例子中,若所有連桿都是在同一平面上運動,稱為平面連桿。若其中至少有一個連桿是在三維空間下運動,稱為空間連桿。機器人系統的骨架即為空間連桿。這些系統的幾何設計要透過计算机辅助设计軟體進行。
歷史
阿基米德[2]應用幾何學來研究連桿。在1500年代時,阿基米德及亚历山大港的希罗的研究是機械理論的主要來源。列奥纳多·达·芬奇則發明了許多的機器以及機構[3]。
瓦特蒸汽機在1700年代中期有相當的重要性。詹姆斯·瓦特理解到若用不同的氣缸處理蒸氣的膨脹及凝結,其效率可以提昇。這讓他開始尋找可以將旋轉運動轉換為直線運動的機構,他發明的機構稱為瓦特連桿。這開始了如何用連桿產生直線(或近似直線)的研究,也讓數學家詹姆斯·約瑟夫·西爾維斯特發明了波塞利耶-利普金机械,可以將旋轉運動轉換為真正的直線[4]。
西爾維斯特的研究也影響了A. B. Kempe,他證明了可以在一系統中將加法及乘法結合,讓系統可以追蹤特定的代數曲線[5]。Kempe的設設計方式產生了電腦科學以及幾何學共同領域的研究[6][7]。
1800世紀末的F. Reuleaux、A. B. W. Kennedy、L. Burmester將連桿系統的分析及合成由画法几何來進行,而巴夫努提·列沃维奇·切比雪夫開創了研究以及發明連桿的解析技巧[4]。
1900年代中期的F. Freudenstein和G. N. Sandor[8]用新開發的數位電腦來求解連桿的方程式,並針對特定功能的需求決定其尺寸,開始了連桿的電腦輔助設計。二十年後這些電腦技術是複雜機械系統分析[9][10]以及機器手臂控制分析中 [11]不可或缺的一部份。
R. E. Kaufman[12][13]結合了電腦快計算多項式方式根的能力,以及圖形化介面,配合Reuleaux的幾何方法及Burmester理論,產生了Freudenstein技巧,並且形成了KINSYN,是互動式連桿設計的電腦繪圖程式。
连杆的現代研究包括機器人、工具機中鉸接系統(articulated systems)的分析及設計,以及線纜驅動和張力系統的分析及設計。這些技術可以應用在生物系統中,甚至是蛋白質的研究。
可動性
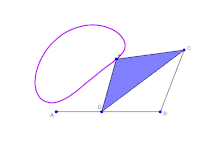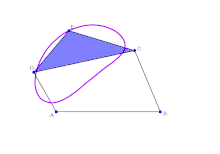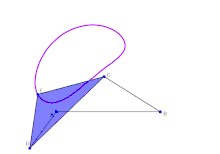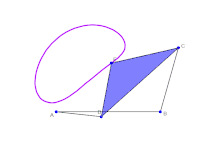
由理想轉動副連接剛體連桿形成的系統,可以由一組的組態參數來定義其位置,例如在轉動副上連桿旋轉的角度,或是移動副上滑塊相對鄰近連桿的距離。由於連桿的幾何限制,只要有組態參數中的最小集,即可計算所有的組態參數。最小集即為「輸入參數」。輸入參數的個數稱為連桿系統的可動性(mobility)或自由度。
由n個剛體組成的系統,相對於固定架,會有6n個自由度。若將固定架也算在內,剛體個數N = n + 1,而可動性M = 6(N − 1),可動性不受選擇哪一個剛體為固定架所影響。
連接剛體的連接會讓系統的自由度以及可動性減少。轉動副和移動副會增加五個限制條件,因此自由度會減5,為了方便起見,可以將連接的限制條件數c用連接的自由度f來表示,c = 6 − f。若以轉動副和移動副的例子來看,其自由度為1,f = 1,因此c = 6 − 1 = 5。
因此,n個可動連桿以及j的連接(其自由度分別為fi, i = 1, ..., j)的連桿系統,可動性可以計算如下
其中的N是包括固定桿件的數量。這稱為Chebychev–Grübler-Kutzbach公式。
有二個重要的特例:簡單開放運動鍵(simple open chain)及簡單封閉運動鍵(simple closed chain)。
簡單開放運動鍵中包括n個可動件,各可動件的端點由j個連接相連,其中一個連到固定桿,因此,N = j + 1,可動性為
簡單封閉運動鍵中包括n個可動件,各可動件的端點由n+1個連接相連,有二個連接接到固定桿,形成一封閉迴路。此時,N=j,可動性為
簡單開放運動鍵的例子是串聯的機械手臂。機械手臂由許多連桿組成,有六個單一自由度的轉動副或移動副組成,因此系統有6個自由度。
簡單封閉運動鍵的例子是由二個轉動副(R)和二個移動副(S)組成的RSSR空間四連桿。三個連接的自由度總和為8,因此連桿的自由度為2
連接
连杆机构最常見的連接是轉動副(旋轉接點,可以簡稱為R)以及移动副(稜柱接點、滑塊,可以簡稱為P)。其他空間連桿中常見連接都可以用轉動副及移动副的組合來表示,例如
連桿的分析及合成
分析連桿的主要數學工具是系統的動態方程式。是一連串的剛體變換,延著串聯的運動鏈,會讓浮動連桿相對固定座可以定位。可以找到一組方程式說明各連桿的位置,也滿足系統的參數。此方程式是非線性方程式,用系統的輸入參數來求得系統的所有組態參數。
Ferdinand Freudenstein有發展一種方,用上述的方程式設計平面四連桿,來達到輸入參數以及連桿組態之間的特定關係。另一種設計平面四連桿的方式是由Ludwig Burmester所發明的,稱為Burmester理論。
平面單自由度連桿
可動性公式提供一種決定單自由度連桿的連桿數以及機械連接的方式。若需要讓平面連桿的自由度M = 1,而fi = 1,其結果為
或
由公式可知連桿數一定要是偶數,
- N = 2, j = 1:這是二桿的连杆,稱為杠杆;
- N = 4, j = 4:這是平面四杆机构;
- N = 6, j = 7:這是六桿連桿。其中有二個連桿上面有三個機械連接, 稱為三接頭桿(ternary links),依三接頭桿位置的不同,有二種組態,若二個三接頭桿是以一個機械連接相接,稱為Watt拓樸,,若二個三接頭桿是以一個連桿相接,稱為Stephenson拓樸[14]。
- N = 8, j = 10:八桿連桿有16種不同的拓樸
- N = 10, j = 13:十桿連桿有230種不同的拓樸
- N = 12, j = 16:十二桿連桿有6856種不同的拓樸。
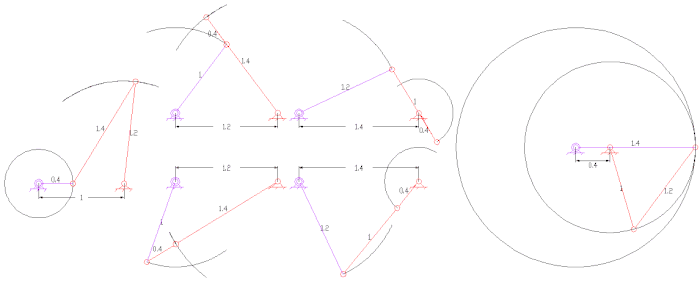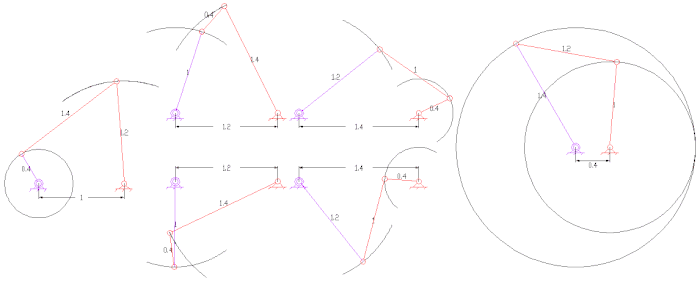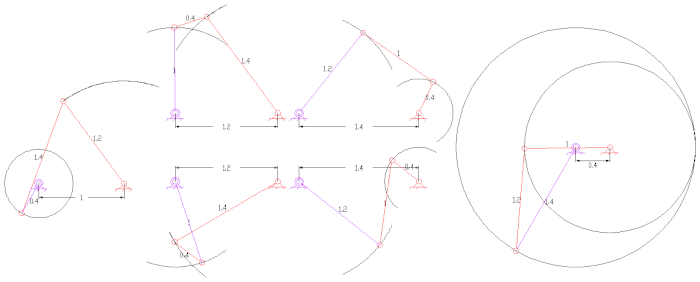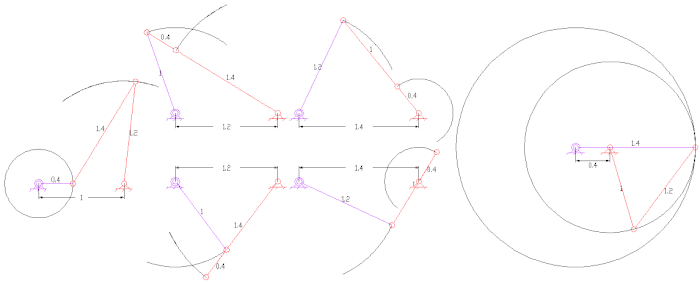
平面四杆机构是最簡單及常見的连杆,也是單自由度系統。以下是一些平面四杆机构的例子
- 曲柄搖桿機構(crank-rocker),輸入桿可以整周旋轉(曲柄),輸出桿只能一定角度內的轉動(搖桿)。
- 雙曲柄搖桿機構(double crank),輸入桿及輸出桿都可以整周旋轉。(曲柄),輸出桿只能一定角度內的轉動(搖桿)。
旋轉對也可以變為移動對,即為曲柄滑塊機構。
其他特殊的連桿
.gif)
- 縮放儀(四桿,2自由度)
- 五桿連桿多半會在兩桿之間加上齒輪咬合,因此形成單自由度的連桿。傳送功率的能力比四連桿強,而且設計的可變性較大。
- Jansen連桿是八桿的腿形機構,是由Theo Jansen所發明的,有用在仿生獸上
- Klann連桿是六桿的腿形機構
- 肘節機構(Toggle mechanism)也是四桿機構,有特別的尺寸設計,在行程的末端,可以在輸入很小力的情形下,有很大的輸出力。可以用在鉗子上。
直線運動機構
- 瓦特的平行運動連桿及瓦特連桿。
- 波塞利耶-利普金机械,第一個可以由旋轉運勳產生完美直線平面連桿機構,有8個連桿,自由度為1。
- Scott Russell連桿機構將直線運動轉換為和其垂直,幾乎是直線的運動。
- 切比雪夫連桿機構,用四連桿連構產生接近直線的軌跡。
- 霍肯連桿機構,用四連桿連構產生接近直線的軌跡。
- 薩魯斯連桿機構,讓兩個表面在保持互相垂直的情形下運動。
- 哈特倒置器,在沒有滑塊的情形下可以產生完美的直線[15]
生物內的連桿
連桿系統也常見於動物身上。Mees Muller提供了有關動物身上各種連桿最完整的敘述[16],他也設計了新的分類系統,特別適合用在生物系統上。其中一個例子是膝蓋的十字韌帶。
生物連桿和工程上的連桿有一個很大的差異:生物連桿很少有轉動件,而且因為一些額外的結構限制(例如需要讓血液及神經通過),其理論的運動範圍可能不大[17]。生物連桿多半是柔性机构。其中的一個或多個連桿是由韌帶構成,連桿多半是三維的。目前已經發現有耦合連桿機構,也有五桿、六桿甚至七桿的連桿[16]。最常見的還是四杆机构。
在動物的關節中常會看到連桿,例如四足類的膝蓋、綿羊的踝關節、鸟和爬行动物的顱機構,後者讓鳥類的上喙可以往上運動。
连杆机构也常見於硬骨魚的魚頭,例如隆頭魚科,有許多特別的水中捕食機構,特別是下頜前突的连杆机构。針對吸取進食,也是四桿機構讓嘴張開,同時和頰腔的3-D擴張。其他的連桿和前上頜骨的突出有關。
连杆机构在生物體也會作為鎖定機構,因此動物可以在肌肉不收縮的情形下可以站著睡覺。有些硬骨魚會pivot feeding,也是靠四連桿的鎖定機構。鎖定機構釋放,讓頭往上,在5至10ms內咬住獵物。
圖輯
.gif) 搖桿-滑塊的函數產生器,可以在1 < u < 10的範圍內計算Log(u)
搖桿-滑塊的函數產生器,可以在1 < u < 10的範圍內計算Log(u).gif) 搖桿-滑塊的函數產生器,可以在0 < u < 45°的範圍內計算Tan(u)
搖桿-滑塊的函數產生器,可以在0 < u < 45°的範圍內計算Tan(u) 四連桿的固定和移動中心
四連桿的固定和移動中心 齒輪齒條式四連桿
齒輪齒條式四連桿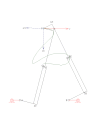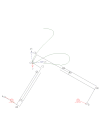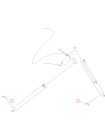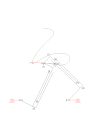 RTRTR機構
RTRTR機構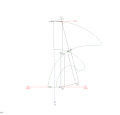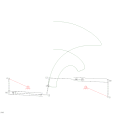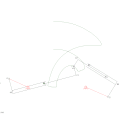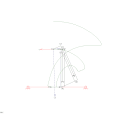 RTRTR機構
RTRTR機構 齒輪五連桿機構
齒輪五連桿機構 3D滑塊曲軸機構
3D滑塊曲軸機構 動畫的Pinochio
動畫的Pinochio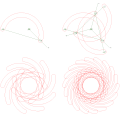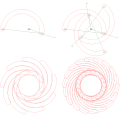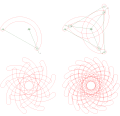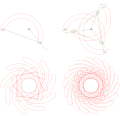
 Crawford二次曲线规
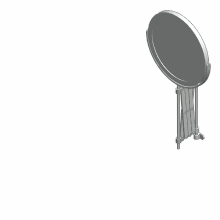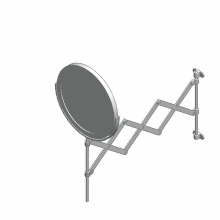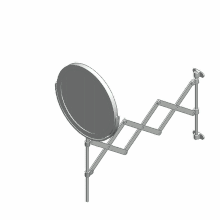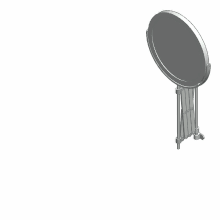
Crawford二次曲线规 向外折疊展開機構
向外折疊展開機構 向內折疊展開機構
向內折疊展開機構
相關條目
參考資料
- Moubarak, P.; Ben-Tzvi, P. . ASME Journal of Mechanisms and Robotics. 2013, 5 (1): 011010. doi:10.1115/1.4023178.
- Koetsier, T. . Mechanism and Machine Theory. 1986, 21 (6): 489–498. doi:10.1016/0094-114x(86)90132-1.
- A. P. Usher, 1929, A History of Mechanical Inventions, Harvard University Press, (reprinted by Dover Publications 1968)
- F. C. Moon, "History of the Dynamics of Machines and Mechanisms from Leonardo to Timoshenko," International Symposium on History of Machines and Mechanisms, (H. S. Yan and M. Ceccarelli, eds.), 2009. doi:10.1007/978-1-4020-9485-9-1
- A. B. Kempe, "On a general method of describing plane curves of the nth degree by linkwork," Proceedings of the London Mathematical Society, VII:213–216, 1876
- Jordan, D.; Steiner, M. . Discrete and Computational Geometry. 1999, 22 (2): 297–315. doi:10.1007/pl00009462. 已忽略未知参数
|doi-access=(帮助) - R. Connelly and E. D. Demaine, "Geometry and Topology of Polygonal Linkages," Chapter 9, Handbook of discrete and computational geometry, (J. E. Goodman and J. O'Rourke, eds.), CRC Press, 2004
- Freudenstein, F.; Sandor, G. N. . ASME Journal of Engineering for Industry. 1959, 81 (2): 159–168. doi:10.1115/1.4008283.
- Sheth, P. N.; Uicker, J. J. . ASME Journal of Engineering for Industry. 1972, 94 (2): 454–464. doi:10.1115/1.3428176.
- C. H. Suh and C. W. Radcliffe, Kinematics and Mechanism Design, John Wiley, pp:458, 1978
- R. P. Paul, Robot Manipulators: Mathematics, Programming and Control, MIT Press, 1981
- R. E. Kaufman and W. G. Maurer, "Interactive Linkage Synthesis on a Small Computer", ACM National Conference, Aug.3–5, 1971
- A. J. Rubel and R. E. Kaufman, 1977, "KINSYN III: A New Human-Engineered System for Interactive Computer-aided Design of Planar Linkages," ASME Transactions, Journal of Engineering for Industry, May
- Tsai, Lung-Wen. . 19 September 2000 [2013-06-13]. ISBN 9781420058420.
- (PDF).
- Muller, M. . Phil. Trans. R. Soc. Lond. B. 1996, 351 (1340): 689–720. PMID 8927640. doi:10.1098/rstb.1996.0065.
- Dawkins, Richard. . Sunday Times. November 24, 1996 [2008-10-29]. (原始内容存档于February 21, 2007). 已忽略未知参数
|url-status=(帮助) - Simionescu, P.A. 1st. Boca Raton, FL: CRC Press. 2014. ISBN 978-1-4822-5290-3.
- Simionescu, P.A. (PDF). ASME 2016 Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Charlotte, NC, USA: 1–10. 21–24 August 2016 [7 January 2017].
- Simionescu, P.A. . International Journal of Mechanisms and Robotic Systems. 2016, 3 (1): 60–79 [2 January 2017]. doi:10.1504/IJMRS.2016.077038. 已忽略未知参数
|doi-access=(帮助)
延伸閱讀
- Bryant, John; Sangwin, Chris. . Princeton: Princeton University Press. 2008: 306. ISBN 978-0-691-13118-4. — Connections between mathematical and real-world mechanical models, historical development of precision machining, some practical advice on fabricating physical models, with ample illustrations and photographs
- Erdman, Arthur G.; Sandor, George N. . Prentice-Hall. 1984. ISBN 0-13-572396-5.
- Hartenberg, R.S. & J. Denavit (1964) Kinematic synthesis of linkages, New York: McGraw-Hill — Online link from Cornell University.
- Kidwell, Peggy Aldrich; Amy Ackerberg-Hastings; David Lindsay Roberts. . Baltimore: Johns Hopkins University Press. 2008: 233–242. ISBN 978-0-8018-8814-4. — "Linkages: a peculiar fascination" (Chapter 14) is a discussion of mechanical linkage usage in American mathematical education, includes extensive references
- How to Draw a Straight Line — Historical discussion of linkage design from Cornell University
- Parmley, Robert. (2000). "Section 23: Linkage." Illustrated Sourcebook of Mechanical Components. New York: McGraw Hill. ISBN 0-07-048617-4 Drawings and discussion of various linkages.
- Sclater, Neil. (2011). "Linkages: Drives and Mechanisms." Mechanisms and Mechanical Devices Sourcebook. 5th ed. New York: McGraw Hill. pp. 89–129. ISBN 978-0-07-170442-7. Drawings and designs of various linkages.