锥台
在几何学中,锥台又称平截头体,指的是圆锥或棱锥被两个平行平面所截后,位于两个平行平面之间的立体。根据所截的是圆锥还是棱锥,可分为圆台与棱台。
| 錐台 | |
|---|---|
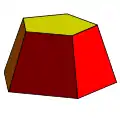 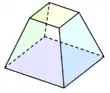 [[Image:|240px|锥台]] [[Image:|240px|锥台]]例如:五角錐台與四角錐台 | |
| 類別 | 錐台 |
| 面 | n+2 |
| 邊 | 3n |
| 頂點 | 2n |
| 歐拉特徵數 | F=n+2, E=3n, V=2n (χ=2) |
| 面的種類 | n 个梯形, 2 个n'边形 |
| 對稱群 | Cnv, [1,n], (*nn) |
| 對偶 | 不對稱雙錐體 |
| 特性 | 凸多面体 |
 | |
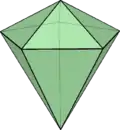 不對稱雙錐體 (對偶多面體) |
 (展開圖) |
公式
体积公式
棱台或圆台的体积是原立体图形的体积减去被截去部分的体积:
B1 指一个底面的面积,B2指另一个底面的面积, and h1, h2 指原顶点分别到两底面的面积。 考虑到
这个体积也可用平截头体的高 h = h2−h1 与两底面面积的希罗平均数表达:
亚历山大里亚的希罗 推导出了这个公式并且凭借它遇到了虚数。[1]
特别地, 圆台的体积是
π 等于 3.14159265...,'R1, R2 是两底面的半径。

Pyramidal frustum.
底面为n边形的棱台的体积是
a1 与 a2 是底面的边长。
表面积公式
对于一个正圆台,[2]
Lateral Surface Area指侧面积,Total Surface Area指总面积,R1 and R2 为底面半径,s 为平截头体的斜高。 一个底面为正n边形的正棱台的表面积是
a1 与 a2是两底面的边长。
参考资料
链接
| 查询維基詞典中的。 |
| 维基共享资源中相关的多媒体资源:锥台 |
- Derivation of formula for the volume of frustums of pyramid and cone (Mathalino.com)
- 埃里克·韦斯坦因. . MathWorld.
- 埃里克·韦斯坦因. . MathWorld.
- Paper models of frustums (truncated pyramids)
- Paper model of frustum (truncated cone)
- Design paper models of conical frustum (truncated cones)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
