鞍點

廣義而說，一個光滑函數（曲線，曲面，或超曲面）的鞍點鄰域的曲線，曲面，或超曲面，都位於這點的切線的不同邊。

${\displaystyle z=x^{2}-y^{2}\,}$的鞍點在 (0,0)

一個不是局部極值點的駐點稱為鞍點。

參考右圖，鞍點這詞語來自於不定二次型${\displaystyle x^{2}-y^{2}\,}$的二維圖形，像個馬鞍：在x-軸往上曲，在y-軸往下曲。

检验二元实函数F(x,y)的驻点是不是鞍点的一个简单的方法，是计算函数在这个点的黑塞矩阵：如果該矩陣行列式小于0，则该点就是鞍点。例如，函数${\displaystyle z=x^{2}-y^{2}}$在驻点${\displaystyle (0,0)}$的黑塞矩阵是：

${\displaystyle {\begin{bmatrix}2&0\\0&-2\\\end{bmatrix}}}$

我们可以看到此矩阵有两个特征值2，－2。它的行列式小於0，因此，这个点是鞍点。然而，这个条件只是充分条件，例如，对于函数${\displaystyle z=x^{4}-y^{4},}$点${\displaystyle (0,0)}$是一个鞍点，但函数在原点的黑塞矩阵是零矩阵，并不小於0.

对于一般的多元函数,驻点是鞍点的必要条件是该点的海塞矩阵不定.

${\displaystyle y=x^{3}\,}$的鞍點在 (0,0)

如右圖，一維鞍點看起來並不像馬鞍！在一維空間裏，鞍點是駐點·也是反曲點。因為函數圖形在鞍點由凸轉凹，或由凹轉凸，鞍點不是區域性極點。

思考一個只有一個變數的函數。這函數在鞍點的一次導數等於零，二次導數換正負符號·例如，函數 ${\displaystyle y=x^{3}\,}$就有一個鞍點在原點。

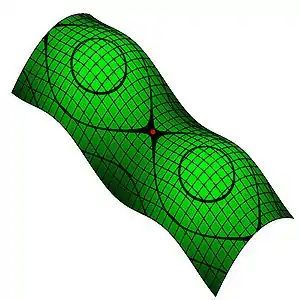
兩座山中間的鞍點（雙紐線的交叉點）

思考一個擁有兩個以上變數的函數。它的曲面在鞍點好像一個馬鞍，在某些往上曲，在其他往下曲。在一幅等高線圖裏，一般來說，當兩個等高線圈圈相交叉的地點，就是鞍點。例如，兩座山中間的山口就是一個鞍點。