曲面
在数学(拓扑学)中,一个曲面(surface)是一个二维流形。三维空间中的例子有三维实心物体的边界。流体的表面,例如雨滴或肥皂泡是一种理想化的曲面。关于雪花的表面,它有很多精细的结构,超越了这个简单的数学定义。关于实际的曲面的资料,请参看表面张力,表面化学,曲面能量。
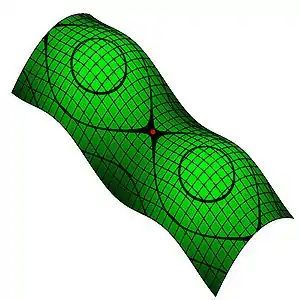
显示了X-, Y-, Z-轮廓的一个开曲面。
定义
在下文中,所有曲面视为第二可数2-维流形。
更精确一点的讲:一个拓扑(带边界)曲面是一个豪斯多夫空间,其中每点有一个开邻域同胚于或者一个E2的开子集或者E2的闭的一半的开子集。
有一个同胚于En的开子集的点的集合称为流形的内部;它总是非空的。内部的补集称为边界;它是一个(1)流形,或者说闭曲线的并集。
无边界的曲面称为闭的,如果它是紧的,否则称为开。
闭曲面分类
紧曲面
带边界紧曲面就是有一个或多个开圆盘被取掉的曲面,而且这些圆盘的闭包互不相交。
在R3中的嵌入
一个紧曲面可以嵌入到R3,只要它可定向或有非空边界。Whitney嵌入定理的结果表明任何曲面可以嵌入R4.
一些模型
把下面这些的边贴起来可以得到一些模型:
* * B B
v v v ^ *>>>>>* *>>>>>*
v v v ^ v v v v
A v v A A v ^ A A v v A A v v A
v v v ^ v v v v
v v v ^ *<<<<<* *>>>>>*
* * B B
球面 实射影平面 克莱因瓶 环面 (打了孔的莫比乌斯带) (面包圈)
基本多边形
每个闭曲面可以从一个偶数边可定向多边形通过将边成对等同构造出来,该多边形称为基本多边形。
这个构造可以用一串长度2n的包含n个不同符号的字符串表示,每个符号出现两次,可以带+1或-1指数。指数-1表示该边的方向和基本多边形的方向相反。
上面的模型可作如下描述:
- 球面:
- 射影平面:
- 克莱因瓶:
- 环面:
(细节请见基本多边形。)
曲面的连通和
给定两个曲面M和M',他们的连通和(connected sum) M # M' 可以通过在每个曲面上除去一个圆盘再把他们在新的边界分量上粘起来。
我们采用下面的记号。
- 球:S
- 环:T
- 克莱因瓶:K
- 射影平面:P
一些结果:
- S # S = S
- S # M = M
- P # P = K
- P # K = P # T
我们用一些缩略记法:nM = M # M # ... # M(n次)以及 0M = S.
闭曲面可以分类如下:
- gT(g-叠环):亏格为g的可定向曲面。
- gP(g-叠射影平面):亏格为g的不可定向曲面。
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
