拐点
.svg.png.webp)
y=x3的函數圖形,原點是其拐點
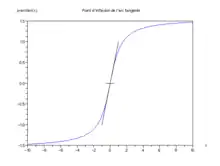
反正切函數的拐點
拐點(英語:)或稱,是一條连续曲線改變凹凸性的點,或者等價地說,是使切線穿越曲線的點。
決定曲線的拐點有助於理解曲線的外形,這在描繪曲線圖形時特別有用。
定義
| 系列條目 | |||||
| 微积分学 | |||||
|---|---|---|---|---|---|
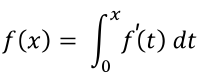 | |||||
| |||||
|
基础概念(含极限论和级数论)
|
|||||
|
一元微分
|
|||||
|
多元微积分
|
|||||
若曲線圖形在一點由凸轉凹,或由凹轉凸,則稱此點為拐點。直觀地說,拐點是使切線穿越曲線的點。
若該曲線圖形的函數在某点的二阶導數為零或不存在,且二阶导数在该点两侧符号相反,该点即为函数的拐点。這是尋找拐點時最實用的方法之一。
拐点的充要条件
拐点的必要条件:设在内二阶可导,,若是曲线的一个拐点,则。 比如,,有,但是0两侧全是凸,所以0不是函数的拐点。
拐点的充分条件:设在内二阶可导,,若在两侧附近异号,则点为曲线的拐点。否则(即保持同号),不是拐点。
參數曲線的拐點
平面參數曲線的拐點是使其曲率變號的點,此時曲率中心(居於曲線凹側)從曲線的一側換至另一側。
雙正則點與拐點
雙正則點是使得參數曲線的一階與二階微分(它們是向量)線性獨立的點。在雙正則點上,曲線既無拐點亦非直線。在非雙正則點上曲率為零,但是不一定有變號。在尋找參數曲線的拐點時,我們通常先以微分找出非雙正則點,繼之研究其局部性狀,以判定是否為拐點。
註:某些作者偏好將拐點定義為「使一階與二階微分平行的點」,在此定義下,切線不一定在該點穿越曲線本身。
文獻
- Robin Hartshorne (1997). Algebraic Geometry. Springer-Verlag. ISBN 0-387-90244-9.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
