反函数及其微分
在数学中,对函数 进行逆运算的功能,在某种程度上,"抵消" 的作用 (准确定义请参阅反函数)。的反函数记作。y = f(x) 和 x = f −1(y)所表示含义相同。
公式:
例如任意的 :
例如任意的 :
它们的两个导数(假设存在),是可逆的,正如莱布尼兹符号所示
这链式规则的直接结果,因为
相对于 的导数为1。
使用拉格朗日记法明确表达 和 的依赖关系和微分。反函数的导数为
该表述等价于
其中 表示一元微分算子 (在函数的空间上), 表示二元复合算子。
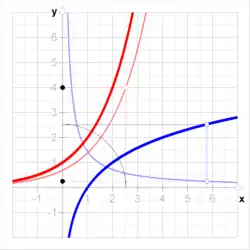
几何上,函数和反函数有关于直线 y = x.镜像的图像, 这种映射将任何线的斜率变成其倒数。
假设 在的邻域有一个反函数并且它在该点的导数不为零,则它的反函数保证在 x 处是可微的, 并有上述公式给出的导数。
反函数举例
- ( 为正)具有逆 中。
但是,在 x = 0有一个问题:平方根函数图像变为垂直的,相对应平方函数的水平切线。
- ( 为实数)具有逆 ( 为正值)
高阶导数
上面给出的链式法则是通过对等式关于微分得到的。对于更高阶的导数,我们可以继续同样的过程。对恒等式对求导两次,得到
使用链式法则进一步简化为
用之前得到的恒等式替换一阶导数,我们得到
对三阶导数类似:
或者用二阶导数的公式,
这些公式是由Faa di Bruno公式推广。
这些公式也可以用拉格朗日表示法来表示。如果和是互逆的,则
反函数的微分举例
- 有逆运算。 使用反函数的二次导数公式,
于是,
- ,
与直接计算相同。
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
