邻域
在拓扑学和相关的数学领域中,邻域是拓扑空间中的基本概念。直觉上说,一个点的邻域是包含这个点的集合,並且該性質是外延的:你可以稍微“抖动”一下这个点而不离开这个集合。
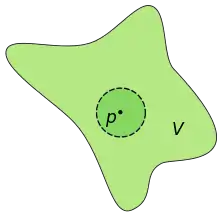
在平面上集合V是点p的邻域,如果围绕p小圆盘包含在V中。

矩形不是它的任何一角的邻域。
在集合论中,邻域指以点 a 为中心的任何开区间,记作:U(a)。
定义
在集合论中,有以下几种邻域:
- 邻域:
- 去心邻域:
- 左邻域:
- 右邻域:
在拓扑学中,拓扑空间X,A,B⊆X,称B是A的邻域,当且仅当以下条件之一成立:
- 存在开集C,使得A⊆C⊆B。
- A⊆Bo。(Bo是B的内部)
- 开邻域,闭邻域
- 若B是开集,则B称为A的开邻域;若B是闭集,则B称为A的闭邻域。
- 邻域系统
- 设x∈X,则{x}所有邻域的集合U(x),称为x(或{x})的邻域系。
注意:某些作者要求邻域是开集,所以在阅读文献时注意约定是很重要的。
如果S是X的子集,S的邻域是集合V,它包含了包含S的开集U。可得出集合V是S的邻域,当且仅当它是在S中的所有点的邻域。
鄰域的度量空间定義
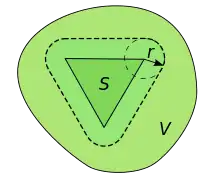
平面上的集合S和S的一致邻域V。
在度量空间M = (X,d)中,集合V是点p的邻域,如果存在以p为中心和半径为r的开球,
它被包含在V中。
一致邻域
V叫做集合S的一致邻域(uniform neighborhood),如果存在正数r使得对于S的所有元素p,
被包含在V中。
对于r>0集合S的r-邻域是X中与S的距离小于r的所有点的集合(或等价的说是以S中一个点为中心半径为r的所有开球的并集)。
可直接得出r-邻域是一致邻域,并且一个集合是一致邻域当且仅当它包含对某个r值的r-邻域。
參見一致空間。
基于邻域的拓扑
上述定义適用於开集的概念早已定义的情況。有另一种方式来定义拓扑,也就是先定义邻域系统,再定义开集:若集中每个点皆有一個邻域被包含於集中,則為開集。
在X上的邻域系统是滤子N(x)(在集合X上)到每个X中的x的指派,使得
- 点x是每个N(x)中的U的元素,
- 每个N(x)中的U包含某个N(x)中的V使得对于每个V中的y有着U在N(y)中。
可以证明这两个定义是兼容的,就是说从使用开集定义的邻域系统获得的拓扑就是最初的拓扑,反之从邻域系统出发亦然。
引用
- Kelley, John L. . New York: Springer-Verlag. 1975. ISBN 0387901256.
- Bredon, Glen E. . New York: Springer-Verlag. 1993. ISBN 0387979263.
- Kaplansky, Irving. . American Mathematical Society. 2001. ISBN 0821826948.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
