多元正态分布
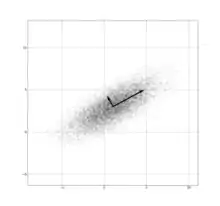 Many samples from a multivariate (bivariate) Gaussian distribution centered at (1,3) with a standard deviation of 3 in roughly the (0.878, 0.478) direction (longer vector) and of 1 in the second direction (shorter vector, orthogonal to the longer vector). 多变量函數 | |
| μ ∈ RN — 位置 Σ ∈ RN×N — 协方差矩阵 (半正定) | |
| 值域 | x ∈ μ+span(Σ) ⊆ RN |
(仅当 Σ 为正定矩阵时) | |
| 累積分布函數 | 解析表达式不存在 |
| 期望值 | μ |
| 眾數 | μ |
| Σ | |
| 熵 | |
| 特徵函数 | |
一般形式
N维随机向量如果服从多变量正态分布,必须满足下面的三个等價条件:
- 任何线性组合服从正态分布。
- 存在随机向量( 它的每个元素服从独立标准正态分布),向量及 矩阵满足.
- 存在和一个对称半正定阵满足的特征函数
注意这里的表示协方差矩阵的行列式。
- 二元的情况
在二维非奇异的情况下(k = rank(Σ) = 2),向量 [X Y]′ 的概率密度函数为:
其中 ρ 是 X 与 Y 之间的相关系数, 且 。在这种情况下,
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.