截對角三方偏方面體
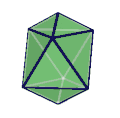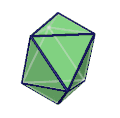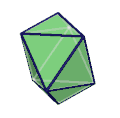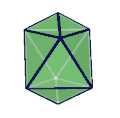
在 幾何學中, 截對角三方偏方面體是截對角偏方面體 這一系列的多面體中的第一個。它有六個五邊形,兩個三角形。
| 截對角三方偏方面體 | |
|---|---|
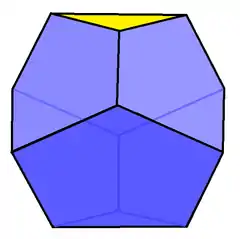 又稱杜勒多面體 | |
| 類別 | 截對角偏方面體 |
| 面 | 8 |
| 邊 | 18 |
| 頂點 | 12 |
| 歐拉特徵數 | F=8, E=18, V=12 (χ=2) |
| 面的種類 | 6個五邊形 2個三角形 |
| 對偶 | 雙三角錐反角柱 |
| 特性 | 凸 |
 雙三角錐反角柱 (對偶多面體) | |
幾何學中
此多面體可透過將一個立方體,或是三方偏方面體,或是一個菱面體,或一個平行六面體中一對處於對角位置的頂點切除,在立方體或著三方偏方面體的例子中,由於截面是平行的,以及原像的高度對稱,因此具有高度的旋轉對稱。
杜勒多面體

《忧郁 I》
這個多面體有時候也稱為杜勒立體或杜勒多面體(Dürer's solid),因為它出現於阿爾布雷希特·杜勒的 1514年畫像《忧郁 I》。這圖像亦稱杜勒圖。
關於杜勒所描述的立體形狀是一些學術辯論的主題。[註 1] 依照Lynch (1982),他假設該立體是一個立方體的截角的誤繪,該點子源於Strauss (1972); 然而大部分的來源資料同意其為菱面體的截角。 儘管有著這樣的同意,而這個菱面體在幾何學中確切的形狀是許多矛盾的理論的主題。
- Richter (1957)聲稱杜勒多面體的原像菱面體中的菱形面的兩條對角線的比是 5:6,而這個數值所產生出來的菱形,其銳角的角度大約為80°[1]。
- Schröder (1980)以及Lynch (1982)在1980年代時認為該菱形對角線長的比應該是而此數值產生出來的菱形,其銳角的角度會變成大約 82°[2][3]。
- MacGillavry (1981)時,測量了該圖形的特徵並測量出該菱形的銳角大約為 79°。他以及一位後來的另一位作者,沃爾夫·馮·恩格爾哈特 (參見 Hideko (2009))認為該角度的形成取決於自然形成的方解石結晶[4]。
- Schreiber (1999)認為根據杜勒的著作,所有的頂點應該是坐落在同一個球面上, 並更進一步的聲明該菱形的銳角為 72°[5]。 Hideko (2009)列舉了其他幾位同樣贊同該菱形銳角為72°的學者,從1955年的保羅·格罗津斯基(Paul Grodzinski)開始。他認為,這種理論的動機少於實際繪圖的分析,而比較傾向關於五邊形以及黃金比例的審美原則[3]。
- Weitzel (2004) 分析了對於同一個立體的1510年的草圖, 從中他確認了薛伯的假設,即該立體有一個 外接球 但菱形的銳角角度會是大約79.5°[2]。
- Hideko (2009)認為該形狀是為了描述一個著名的幾何學問題,倍立方體的解答,而杜勒也在1525年中提到。 他隨後總結出(在兩個頂點截去前)該立體是一個立方體沿著對角線伸長而成的。 更具體地說,他認為杜勒繪製了一個實際的立方體,長對角線平行於圖形平面,然後在長對角線的方向上以因為某種因素而放大他的繪畫:結果會和他繪製一個被延長的圖形相同。放大的因素是因為關於倍立方後的體積是原立方體的 21/3 ≈ 1.253,但秀子導出不同的,為了適應圖紙的放大因素,1.277,以一個更複雜的方式[3]。
- Futamura,Frantz & Crannell (2014)將所提出的解決方案分類為該問題,透過兩個參數:銳角以及切面,稱為交比。 他們估算這個交比很接近麥克·蓋勒艾瑞的,而且具有一個接近 黃金比例的數值。 基於這一點,他們認為銳角是 而交比是精確的 [6]。
註譯
- 參見 Weitzel (2004) 以及 Ziegler (2014),從中得出以下許多歷史事件。
參考資料
- Richter, D. H., , Z. Vermessungswesen, 1957, 82: 284–288 and 350–357. As cited by Weitzel (2004)
- Schröder, E., , Basel, 1980. As cited by Weitzel (2004).
- Lynch, Terence, , Journal of the Warburg and Courtauld Institutes (The Warburg Institute), 1982, 45: 226–232, JSTOR 750979, doi:10.2307/750979
- MacGillavry, C., , Nederl. Akad. Wetensch. Proc. Ser. B, 1981, 84: 287–294. As cited by Weitzel (2004)
- Schreiber, Peter, , Historia Mathematica, 1999, 26: 369–377, doi:10.1006/hmat.1999.2245.
- Futamura, F.; Frantz, M.; Crannell, A., , Journal of Mathematics and the Arts, 2014, 8 (3-4): 111–119, arXiv:1405.6481, doi:10.1080/17513472.2014.974483.
- Strauss, Walter L., , New York: 168, 1972, ISBN 0-486-22851-7. As cited by Lynch (1982).
- Weber, P., , Strassburg, 1900. As cited by Weitzel (2004).
- Weitzel, Hans, , Historia Mathematica, 2004, 31 (1): 11–14, doi:10.1016/S0315-0860(03)00029-6.
- Hideko, Ishizu, (PDF), Aesthetics (The Japanese Society for Aesthetics), 2009, 13: 179–194.
- Ziegler, Günter M., , Alex Bellos's Adventures in Numberland, The Guardian, December 3, 2014.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.