极值定理
在微积分中,极值定理说明如果实函数f在闭区间[a,b]上是连续函数,则它一定取得最大值和最小值,至少一次。也就是说,存在[a,b]内的c和d,使得:
- 对于所有。
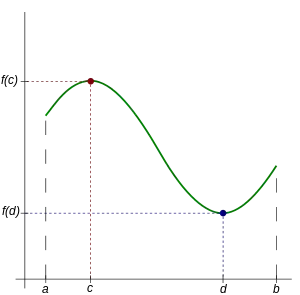
一个相关的定理是有界性定理,它说明闭区间[a,b]内的连续函数f在该区间上有界。也就是说,存在实数m和M,使得:
- 对于所有。
定理的证明
我们来证明f的上界和最大值的存在。把这个结果应用于函数–f,也可推出f的下界和最小值的存在。
我们首先证明有界性定理,它是证明极值定理中的一个步骤。证明极值定理的基本步骤为:
有界性定理的证明
假设函数f在区间[a,b]内連續且没有上界。那么,根据实数的阿基米德公理,对于每一个自然数n,都存在[a,b]内的一个xn,使得f(xn) > n。这便定义了一个序列{xn}。由于[a,b]是有界的,根据波尔查诺-魏尔施特拉斯定理,可推出存在{xn}的一个收敛的子序列{}。把它的极限记为x。由于[a,b]是闭区间,它一定含有x。因为f在x处连续,我们知道{f()}收敛于实数f(x)。但对于所有的k,都有f() > nk ≥ k,这意味着{f()}发散于无穷大。得出矛盾。因此,f在[a,b]内有上界。证毕。
极值定理的证明
我们现在证明函数f在区间[a,b]内有最大值。根据有界性定理,f有上界,因此,根据实数的戴德金完备性,f的最小上界M存在。我们需要寻找[a,b]内的一个d,使得M = f(d)。设n为一个自然数。由于M是最小上界,M – 1/n就不是f的上界。因此,存在[a,b]内的dn,使得M – 1/n < f(dn)。这便定义了一个序列{dn}。由于M是f的一个上界,我们便有M – 1/n < f(dn) ≤ M,对于所有的n。因此,序列{f(dn)}收敛于M。
根据波尔查诺-魏尔施特拉斯定理,可知存在一个子序列{},它收敛于某个d,且由于[a,b]是闭区间,d位于[a,b]内。因为f在d处连续,所以序列{f()}收敛于f(d)。但{f()}是{f(dn)}的一个子序列,收敛于M,因此M = f(d)。所以,f在d处取得最小上界M。证毕。
例子
以下的例子说明了为什么函数的定义域需要是封闭和有界的。
- 定义在[0,∞)的函数f(x) = x没有上界。
- 定义在[0,∞)的函数f(x) = x/(1 + x)有界,但不取得最小上界1。
- 定义在(0,1]的函数f(x) = 1/x没有上界。
- 定义在(0,1]的函数f(x) = 1 –x有界,但不取得最小上界1。
推广到半连续函数
如果把f的连续性减弱为半连续,则有界性定理和极值定理的对应的一半仍然成立,且扩展的实数轴上的值–∞和+∞也可以允许为可能的值。更加精确地:
定理:如果函数f : [a,b] → [–∞,∞)是上半连续的,也就是说,对于[a,b]内的所有x,都有:
- ,
那么f有上界,且取得最小上界。
证明:如果对于[a,b]内的所有x,都有f(x) = –∞,那么最小上界也是–∞,于是定理成立。在任何其它情况下,只需把上面的证明稍加修改便可。在有界性定理的证明中,f在x处的半连续性只意味着子序列{f()}的上极限有上界f(x) < ∞,但这已足以得到矛盾。在极值定理的证明中,f在d处的半连续性意味着子序列{f()}的上极限有上界f(d),但这已足以推出f(d) = M的结论。证毕。
把这个结果应用于−f,可得:
定理:如果函数f : [a,b] → (–∞,∞]是下半连续的,也就是说,对于[a,b]内的所有x,都有:
那么f有下界,且取得最大下界。
一个实函数是上半连续且下半连续的,当且仅当它是连续的。因此,从这两个定理就可以推出有界性定理和极值定理。
参考文献
- Parzynski, William R. . McGraw-Hill, Inc. 1982: 102–104.