棱柱
棱柱是幾何學中的一種常見的三维多面体,指平面上的一个多边形平行投影到与该平面平行的平面所截得的封閉幾何體。棱柱的两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都相互平行。
| 棱柱 | |
|---|---|
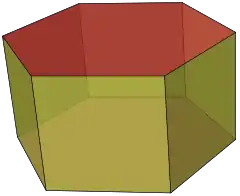 以六角柱為例 | |
| 類別 | 棱柱 |
| 面 | 2+n |
| 邊 | 3n |
| 頂點 | 2n |
| 歐拉特徵數 | F=2+n, E=3n, V=2n (χ=2) |
| 面的種類 | 多邊形 矩形 |
| 頂點圖 | 4.4.n |
| 考克斯特符號 | |
| 施萊夫利符號 | {n}×{} or t{2, n} |
| 對稱群 | Dnh, [n,2], (*n22), order 4n |
| 對偶 | 雙n角錐 |
| 旋轉對稱群 | Dn, [n,2]+, (n22), order 2n |
| 特性 | 凸、semi-regular、vertex-transitive |
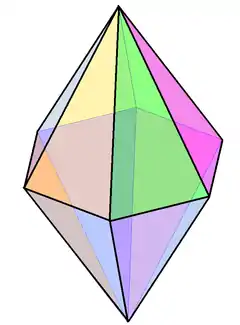 雙n角錐 (對偶多面體) |
 (展開圖) |

若用於截平行平面的平面數為n,那麼該稜柱便稱為n-稜柱。如三稜柱就是由兩個平行的平面被三個平面所垂直截得的封閉幾何體。
稜柱的各種屬性
底面
棱柱中两个互相平行的面,叫做棱柱的底面。 并且底面与侧面互相垂直。
侧面
棱柱中除两个底面以外的其余各个面都叫做棱柱的侧面。
侧棱
棱柱中两个侧面的公共边叫做棱柱侧棱。
顶点
棱柱中侧面与底面的公共顶点叫做棱柱的顶点。
对角线
棱柱中不在同一平面上的两个顶点的连线叫做棱柱的对角线。
高
棱柱的两个底面的距离叫做棱柱的高。
对角面
棱柱中过不相邻的两条侧棱的截面叫做棱柱的对角面。
體積
假設一個稜柱的底面面積為,高為,那麼這個稜柱的體積為:
一些特殊的棱柱
斜棱柱
侧棱不垂直于底面的棱柱叫做斜棱柱,画斜棱柱时,一般将侧棱画成不与底面垂直。
直棱柱
侧棱垂直于底面的棱柱叫做直棱柱。画直棱柱时,应将侧棱画成与底面垂直。
正棱柱
底面是正多边形的直棱柱叫做正棱柱。[1]
參見
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
