满射
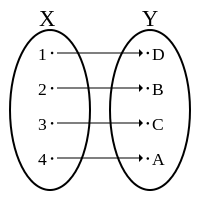
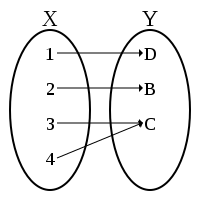
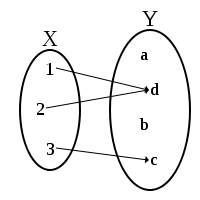
满射或蓋射(英語:),或稱满射函数或映成函數,一个函数为满射,則对于任意的陪域 中的元素 ,在函数的定义域 中存在一點 使得 。换句话说,是满射時,它的值域与陪域相等,或者,等价地,如果每一个陪域中的元素 其原像 不等於空集合。
例子和反例
函数,定义为,不是一个满射,因为,(舉例)不存在一个实数满足。
但是,如果把的陪域限制到只有非负实数,则函数为满射。这是因为,给定一个任意的非负实数,我们能对求解,得到。
|
|
|
|
|
|
性质
參考文獻
- Bourbaki, Nicolas. . Springer. 2004 [1968]. ISBN 978-3-540-22525-6.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.